III. A base e a rolante. O movimento inverso
Suponhamos que o plano móvel  ocupa sucessivamente as
posições
ocupa sucessivamente as
posições
 no plano fixo. Como vimos a passagem de
no plano fixo. Como vimos a passagem de
 para
para
 faz-se
através de uma rotação em torno de um certo ponto
faz-se
através de uma rotação em torno de um certo ponto 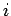 de
de  , a passagem de
, a passagem de
 para
para
 faz-se
através de uma rotação em torno de um certo ponto
faz-se
através de uma rotação em torno de um certo ponto  de
de  e assim sucessivamente. Temos desta
forma uma sucessão de pontos
e assim sucessivamente. Temos desta
forma uma sucessão de pontos  em
em
 - os centros de
rotação
das sucessivas mudanças de
- os centros de
rotação
das sucessivas mudanças de  - que formam uma linha poligonal no
plano fixo.
- que formam uma linha poligonal no
plano fixo.
Seja  o primeiro centro de
rotação, num instante inicial fixo, e consideremos agora
os pontos
o primeiro centro de
rotação, num instante inicial fixo, e consideremos agora
os pontos  do plano
móvel
do plano
móvel  que, nos deslocamentos sucessivos, vêm coincidir com os pontos
que, nos deslocamentos sucessivos, vêm coincidir com os pontos
 de
de
 . Os pontos
. Os pontos
 do plano
móvel
do plano
móvel  , que identificamos com a sua
posição inicial
, que identificamos com a sua
posição inicial  , formam
também uma linha poligonal, agora em
, formam
também uma linha poligonal, agora em
 ,
que passa em
,
que passa em  .
.

No primeiro deslocamento
 roda em torno de
roda em torno de  e o ponto
e o ponto  irá sobrepôr-se ao ponto
irá sobrepôr-se ao ponto
 .
No segundo
deslocamento,
.
No segundo
deslocamento,  roda em torno de
roda em torno de  e o ponto
e o ponto  irá sobrepôr-se ao ponto
irá sobrepôr-se ao ponto
 ,
e assim
sucessivamente. Os segmentos
,
e assim
sucessivamente. Os segmentos  ,
,  ,
,  , da poligonal móvel vão pois
aplicar-se sucessivamente sobre segmentos
, da poligonal móvel vão pois
aplicar-se sucessivamente sobre segmentos  ,
,  ,
,  , da poligonal fixa, isto é, a
poligonal
, da poligonal fixa, isto é, a
poligonal  "rola" sobre a poligonal
"rola" sobre a poligonal
 . Temos assim um
movimento em que uma linha poligonal de
. Temos assim um
movimento em que uma linha poligonal de  rola (sem deslizar) sobre uma outra
linha poligonal de
rola (sem deslizar) sobre uma outra
linha poligonal de  , como se ilustra nas
animações seguintes:
, como se ilustra nas
animações seguintes:
Estas considerações, no argumento limite em que as
diversas posições estão infinitesimalmente
próximas, permitem concluir que:
O movimento
contínuo de um plano móvel
 sobre um plano fixo sobre um plano fixo
 , pode ser gerado pelo
rolamento (sem
deslizamento) de uma curva do plano móvel (a rolante) sobre uma curva do plano
fixo (a base). , pode ser gerado pelo
rolamento (sem
deslizamento) de uma curva do plano móvel (a rolante) sobre uma curva do plano
fixo (a base). |
Cada uma dessas curvas pode ser definida como o lugar geométrico
dos centros instantâneos de rotação, no plano
móvel e no plano fixo  e
e  , respectivamente.
, respectivamente.
Uma pequena nota - aqui excluímos o caso de um movimento de translacção e o caso em que o centro instantâneo de rotação está fixo durante um intervalo de tempo finito.
 a deslocar-se sobre
a deslocar-se sobre
 . É claro que,
para um
observador que esteja rigidamente ligado ao plano
. É claro que,
para um
observador que esteja rigidamente ligado ao plano
 , é o plano
, é o plano
 que se desloca
relativamente a
que se desloca
relativamente a  . Este movimento, que representamos
por
. Este movimento, que representamos
por 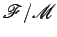 ,
diz-se, por isso, o movimento inverso do movimento
,
diz-se, por isso, o movimento inverso do movimento
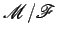 .
.
Se o movimento é contínuo, todo o ponto  de
de  descreve uma curva
descreve uma curva
 em
em
 . No movimento inverso
a curva
. No movimento inverso
a curva 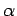 passará empre por
passará empre por  .
Anàlogamente, se uma curva
.
Anàlogamente, se uma curva 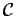 de
de  passa sempre por um certo ponto fixo
de
passa sempre por um certo ponto fixo
de  , este ponto, no movimento inverso,
descreverá a curva
, este ponto, no movimento inverso,
descreverá a curva 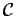 . Isto pode ser usado para obter um duplo
traçado mecânico de curvas. Imaginemos, com efeito, um
marcador fixo em
. Isto pode ser usado para obter um duplo
traçado mecânico de curvas. Imaginemos, com efeito, um
marcador fixo em  . Ele traçará a curva
. Ele traçará a curva
 , mesmo
quando,
estando
, mesmo
quando,
estando  fixo, nós deslocamos o
papel relativamente ao marcador.
fixo, nós deslocamos o
papel relativamente ao marcador.
É claro que os
papéis, desempenhados pela rolante e pela base, trocam, quando
consideramos o movimento inverso. Eis um exemplo, de
interpretação imediata, e que ilustra tudo o que acabamos
de dizer:
|
|
|
- Exemplo 1. Um segmento move-se de tal forma que as suas extremidades estão sempre sobre os lados de um ângulo. Elipsógrafo. Teorema de La Hire
- Exemplo 2. Um ângulo move-se de tal forma que os seus lados são sempre tangenciais a dois círculos dados
- Exemplo 3. Três barras