Resolução gráfica de equações algébricas
João
Nuno Tavares
| Construção de Lill |
||
|
E. Lill publicou em 1867 outra construção gráfica, bastante diferente da apresentada por Segner, mas também muito simples, e que passámos a descrever:
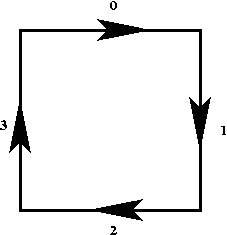

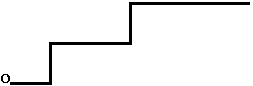

A construção de Lill está esquematizada
nas
figuras anteriores, e ilustrada no applet seguinte,
onde podemos constatar que ela continua válida para coeficientes
negativos e para todo o
valor de x (positivo ou negativo).
No applet, que por simplicidade está
construído para uma equação do 3º grau,
podemos modificar os segmentos
|
|
|
| Ilustração com o Geometer Sketchpad | A construção de Lill está ainda ilustrada na construção seguinte feita com o Geometer Sketchpad. | |
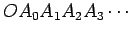 cujos lados
consecutivos são
perpendiculares, e cujos comprimentos são
iguais aos coeficientes (supostos reais) do polinómio:
cujos lados
consecutivos são
perpendiculares, e cujos comprimentos são
iguais aos coeficientes (supostos reais) do polinómio: 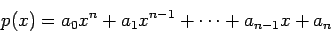
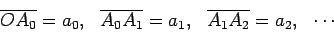
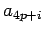 é o do lado
é o do lado 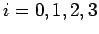 do quadrado acima indicado.
do quadrado acima indicado.
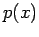 . Assim, por exemplo, nas figuras
seguintes representámos as ortógonas dos
polinómios
. Assim, por exemplo, nas figuras
seguintes representámos as ortógonas dos
polinómios 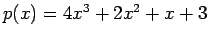 e
e
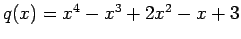 ,
respectivamente.
,
respectivamente. ,
cujos vértices sucessivos
,
cujos vértices sucessivos
 estão, respectivamente, nos
prolongamentos dos segmentos
estão, respectivamente, nos
prolongamentos dos segmentos  ,
,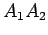 ,
,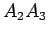 ,
,
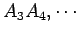 da
ortógona de
da
ortógona de 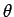 o ângulo
o ângulo
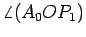 e
designemos por:
e
designemos por: 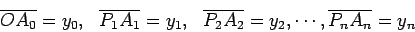
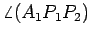 ,
,
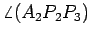 ,
,
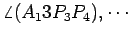 , são todos iguais a
, são todos iguais a 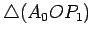 ,
,
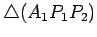 ,
,
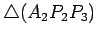 ,
,
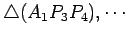 são
todos semelhantes.
Consideremos um deles, por exemplo,
são
todos semelhantes.
Consideremos um deles, por exemplo,
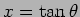 . Temos
então que:
. Temos
então que: 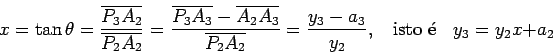
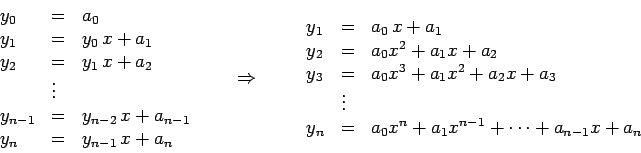
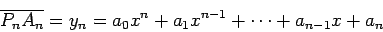
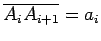 , e o
valor de x, para obter o gráfico de
, e o
valor de x, para obter o gráfico de 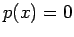 , que são evidentemente
os valores de
, que são evidentemente
os valores de 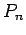 coincide com
coincide com 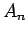 .
.