Seja 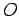 a origem de um sistema de eixos
a origem de um sistema de eixos 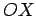 e
e 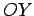 , e
representemos os gráficos das funções:
, e
representemos os gráficos das funções:
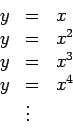
Podemos continuar indefinidamente
esta construção para
graus
superiores. No entanto, vamos apenas limitar-mo-nos à
construção de
parábolas até ao 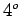 grau, o
que permitirá resolver equações de
grau, o
que permitirá resolver equações de 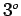 grau,
como veremos.
grau,
como veremos.
Todos estes gráficos passam pelos pontos 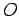 e
e 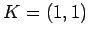 .
Supômos, além disso, que
.
Supômos, além disso, que 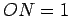 .
Tracemos ainda os gráficos das funções:
.
Tracemos ainda os gráficos das funções:
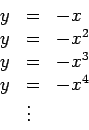
que passam pelos pontos
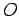 e
e 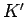 .
.
Consideremos agora uma
régua 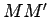 perpendicular ao eixo
perpendicular ao eixo 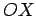 ,
e Imaginemos que se colocam pesos nos pontos
,
e Imaginemos que se colocam pesos nos pontos 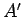 ,
, 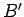 ,
, 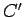 ,
, 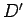 ,
, 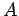 ,
, 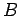 ,
, 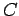 ,
, 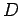 ,
podendo estes deslizar ao longo das curvas já referidas. O
aparelho
assim construído, pode servir para resolver uma
equação de
,
podendo estes deslizar ao longo das curvas já referidas. O
aparelho
assim construído, pode servir para resolver uma
equação de 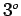 grau, da qual conhecemos os seus coeficientes.
Vejámos como.
grau, da qual conhecemos os seus coeficientes.
Vejámos como.

Consideremos a equação
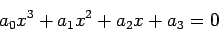
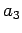 no
ponto
no
ponto 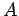 , se
, se 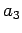 é positivo, ou no ponto
é positivo, ou no ponto 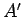 , se
, se 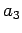 é negativo. De igual modo, suspende-se um peso igual a
é negativo. De igual modo, suspende-se um peso igual a 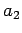 no
ponto
no
ponto 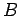 , se
, se 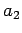 é positivo, ou no ponto
é positivo, ou no ponto 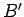 , se
, se 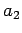 é negativo (os outros dois pesos são suspensos de maneira
análoga). Sendo assim, a régua oscilará em torno
do ponto
é negativo (os outros dois pesos são suspensos de maneira
análoga). Sendo assim, a régua oscilará em torno
do ponto  e quando ficar em equilíbrio,
e quando ficar em equilíbrio, 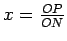 será a
solução procurada
da equação.
será a
solução procurada
da equação. Vejamos por exemplo a equação:
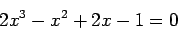
 |
 |
Seja 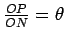 . Tem-se que:
. Tem-se que:
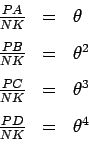
O equilíbrio verifica-se quando a equação
dos
momentos é satisfeita, isto é, quando
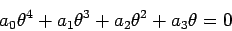
(tendo em conta os respectivos sinais). Tem-se então que:
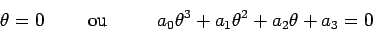
Como
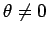 ,
tem-se que
,
tem-se que 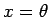 é solução da equação
é solução da equação
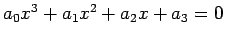 .
.