| Next: Conicógrafo de Crawford Previous: Teorema de Dandelin Contents | |||
|
|
|||
III. Aparelhos para construir cónicas. Conicógrafos
Uma das possíveis definições de cónica, é a seguinte:
No applet seguinte, pode mudar o valor da excentricidade |
|||
|
Com as notações seguintes:
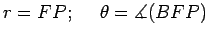
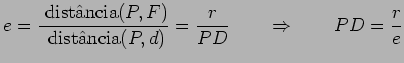
Mas, por outro lado: 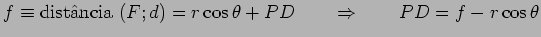 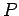 está à esquerda da directriz,
como na figura, de tal forma que está à esquerda da directriz,
como na figura, de tal forma que
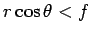 . .
Portanto, nesta situação, virá que:
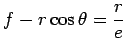
Resolvendo em ordem a 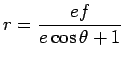
Supondo que 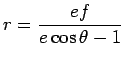
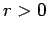 , esta última equação
implica que , esta última equação
implica que 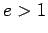 , isto é, existem pontos à direita da directriz
apenas no caso da hipérbole. , isto é, existem pontos à direita da directriz
apenas no caso da hipérbole.
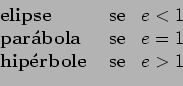
Resumindo:
|
|||
|
|
|||
| Next: Conicógrafo de Crawford Previous: Teorema de Dandelin Contents |
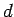 uma linha recta fixa no plano,
uma linha recta fixa no plano, 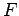 um ponto fixo, não
pertencente a
um ponto fixo, não
pertencente a 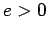 um número positivo.
um número positivo.
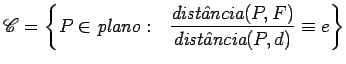
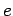 , foco
, foco
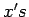 perpendicular à directriz,
como na figura seguinte:
perpendicular à directriz,
como na figura seguinte: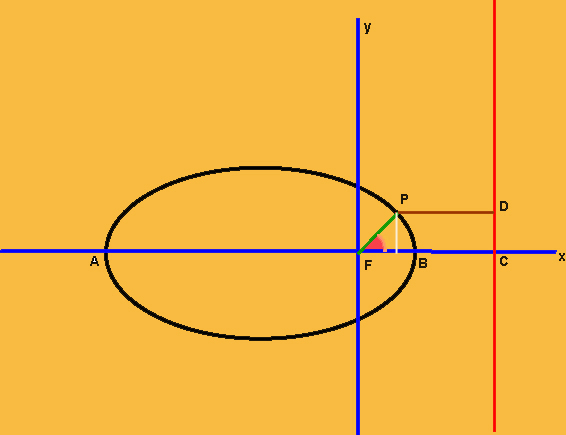
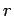 , obtem-se:
, obtem-se:
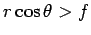 , deduzimos, de
forma análoga, que:
, deduzimos, de
forma análoga, que:

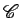 uma cónica com excentricidade
uma cónica com excentricidade 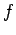 .
.
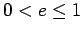 , a cónica
, a cónica