Como Dandelin demonstrou o Teorema
de Pascal (I)
O teorema clássico de Dandelin |
|||||
Um enunciado análogo
é válido para a hipérbole e para a
parábola, obtidas também como secções
cónicas planas de um
cone de revolução (veja os enunciados detalhados e as
demonstrações correspondentes em LINK).)
|
|||||
|
Dada uma secção cónica e uma esfera, tangente ao plano dessa secção cónica num dos seus focos, é sempre possível construir um cone tangente a essa esfera e que contem a secção cónica inicial.  De facto, tomando como exemplo
uma elipse, a figura anterior ilustra
claramente o que há a fazer: seja
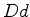 o seu
eixo maior, o seu
eixo maior, 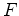 um foco e um foco e 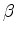 o plano perpendicular ao plano
da
curva que contém o plano perpendicular ao plano
da
curva que contém 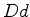 (o plano do papel). Traçamos por (o plano do papel). Traçamos por 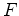 o
círculo de raio igual ao da esfera dada, tangente ao eixo o
círculo de raio igual ao da esfera dada, tangente ao eixo 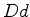 .
Construímos as duas tangentes ao círculo que passam por
.
Construímos as duas tangentes ao círculo que passam por 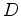 e e
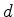 , respectivamente. A
intersecção dessas duas rectas será o
vértice do cone , respectivamente. A
intersecção dessas duas rectas será o
vértice do cone 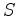 , sendo
, sendo 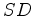 e e  geratrizes do cone. geratrizes do cone. |
|||||
Hiperbolóide de Revolução |
|||||
Consideremos uma
esfera 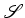 e uma recta e uma recta 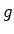 , tangente e
rigidamente fixa à esfera. Rodando a esfera em torno de um dos
seus diâmetros, as sucessivas posições da recta
, tangente e
rigidamente fixa à esfera. Rodando a esfera em torno de um dos
seus diâmetros, as sucessivas posições da recta 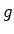 geram uma
superfície que se designa por hiperbolóide de
revolução. O cone
recto é um caso particular do hiperbolóide de
revolução
obtido quando a recta considerada intersecta o referido
diâmetro (eixo de rotação). geram uma
superfície que se designa por hiperbolóide de
revolução. O cone
recto é um caso particular do hiperbolóide de
revolução
obtido quando a recta considerada intersecta o referido
diâmetro (eixo de rotação).
As esferas cujo centro está sobre o eixo de
rotação e que são
tangentes à recta |
|||||
Propriedades do hiperbolóide |
|||||
 |
|||||
|
Demonstração
... Sejam
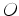 e e  os centros das duas esferas. Estas duas esferas
tocarão o hiperbolóide em duas circunferências os centros das duas esferas. Estas duas esferas
tocarão o hiperbolóide em duas circunferências 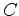 e e 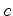 . Por
qualquer ponto
. Por
qualquer ponto 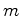 , da intersecção do hiperbolóide com o plano
, da intersecção do hiperbolóide com o plano
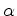 , construímos
arbitrariamente um gerador. Este será
tangente às duas esferas em , construímos
arbitrariamente um gerador. Este será
tangente às duas esferas em 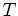 e e 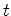 , pontos das
circunferências
, pontos das
circunferências 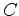 e e 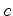 . De seguida, construímos por
. De seguida, construímos por 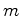 as
rectas as
rectas 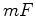 e e 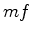 . Como estas rectas são tangentes à
esfera de centro
. Como estas rectas são tangentes à
esfera de centro 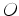 e passam ambas por e passam ambas por 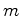 resulta que resulta que
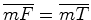 .
Analogamente, .
Analogamente,
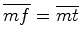 . Consideremos os dois casos
possíveis: . Consideremos os dois casos
possíveis:
No primeiro caso temos que: 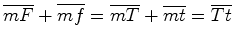
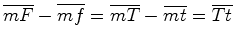
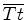 , ou seja, o comprimento da porção do gerador
entre
, ou seja, o comprimento da porção do gerador
entre 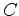 e e 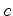 é constante, qualquer que seja o ponto é constante, qualquer que seja o ponto 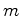 . Assim,
em [1] temos uma elipse de focos
. Assim,
em [1] temos uma elipse de focos 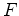 e e 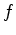 e em [2] uma hipérbole
de focos e em [2] uma hipérbole
de focos 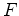 e e 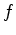 .
.
Note-se que pode ainda acontecer uma única esfera ser
tangente ao
plano
|
|||||
|
|||||
|
Demonstração ...
Construímos uma recta Por cada um dos seus focos construímos uma esfera
tangente ao
plano da cónica e à recta Consideremos a recta que una os centros Fazendo rodar
|
|||||
| Próximo: Demonstração
de Dandelin do Teorema de Pascal (II) Anterior: Corolários do Teorema de Pascal Regresso ao Índice |
|||||
 , e duas esferas tangentes ao plano e ao cone no
seu interior.
, e duas esferas tangentes ao plano e ao cone no
seu interior. 
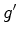 , obtida
por reflexão de
, obtida
por reflexão de 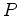 , o que resulta no caso de uma parábola.
, o que resulta no caso de uma parábola.
