Existe um hipercubo (4d)?
João Nuno Tavares


Os cubos de dimensão 1 (segmentos), de dimensão 2 (quadrados) e os de dimensão 3 são familiares:





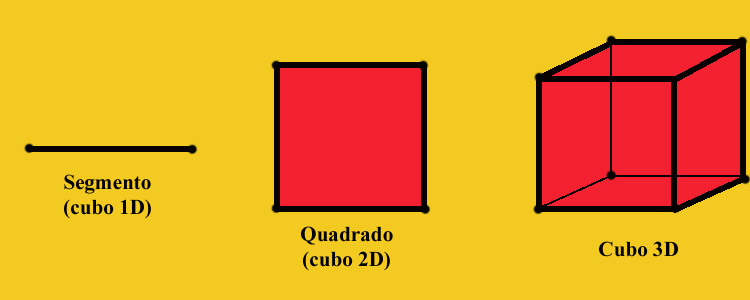
Quantos elementos têm cada um?


Vértices
(Faces 0D)
 Arestas
(Faces 1D)
 Faces 2D
 Faces 3D
 Faces 4D  Total
Segmento
(cubo 1D)
 2
 1


3
Quadrado
(cubo 2D)
 4
 4
 1

9
Cubo 3D
 8
 12
 6
 1
27
Hipercubo 4D
 16
 ?
 ? ?
 1
 81



Parece haver certas regularidades. Por exemplo, o número de vértices aumenta em potências de dois: 2, 4, 8, ... , enquanto que o número total de elementos aumenta em potências de três: 3, 9, 27, ....

Tudo parece indicar que, a manter-se estas regularidades, um hipercubo 4D terá 16 vértices, e um número total de 81 elementos! 

Será assim? E quantas arestas tem? e faces 2D? e faces 3D?

 


Uma maneira de gerar um quadrado (cubo 2d) é a seguinte:

começamos com um segmento (cubo 1D) e "varremos" esse segmento numa direcção perpendicular.		 Por favor habilite Java para uma construção interativa (com Cinderella).




Analogamente, uma maneira de gerar um cubo 3D é a seguinte:

começamos com um quadrado (cubo 2D) e "varremos" esse quadrado numa direcção perpendicular.		 Por favor habilite Java para uma construção interativa (com Cinderella).



Nada impede que prossigamos este método: para gerar um cubo 4D começamos com um cubo 3D e "varremos" esse cubo numa direcção perpendicular.


Por favor habilite Java para uma construção interativa (com Cinderella).



Mas existe um outro processo para "ver" o hipercubo 4D. Comecemos em baixa dimensão.





Quando projectamos um quadrado sobre uma recta, a partir de um ponto exterior,
obtemos um segmento dentro de outro e 4 vértices.
 Por favor habilite Java para uma construção interativa (com Cinderella).





Analogamente, quando projectamos um cubo 3D
sobre um plano, a partir de um ponto exterior,
obtemos um quadrado dentro de outro, 8 vértices,
12 arestas e 6 faces.
 Por favor habilite Java para uma construção interativa (com Cinderella).



Isto leva-nos naturalmente à conjectura de que, quando projectamos um hipercubo 4D sobre o espaço tridimensional, a partir de um ponto exterior, obtemos um cubo 3D dentro de outro, etc...

Por favor habilite Java para uma construção interativa (com Cinderella).



É agora fácil contar o número de elementos de cada tipo no hipercubo 4D, completando assim a tabela anterior


Vértices
(Faces 0D)
 Arestas
(Faces 1D)
 Faces 2D
 Faces 3D
 Faces 4D  Total
Segmento
(cubo 1D)
 2
 1


3
Quadrado
(cubo 2D)
 4
 4
 1

9
Cubo 3D
 8
 12
 6
 1
27
Hipercubo 4D
 16
 32
 24 8
 1
 81



Note um facto interessante: se somarmos os vários elementos de cada um dos cubos, com sinal alternado, obtemos sempre 1:
  • 2 - 1 = 1
  • 4 - 4 + 1 = 1
  • 8 - 12 + 6 - 1 = 1
  • 16 - 32 + 24 - 8 + 1 = 1
A soma da esquerda chama-se a característica de Euler-Poincaré do cubo.




"O interior da quarta dimensão", Max Weber,(1913)



Mas:
  • Existe realmente um hipercubo?
  • Se sim, onde existe? E como existe? Em que sentido?
  • Como sabemos se existe? Podemos estar errados?
  • Se não, como pudemos saber tanto àcerca dos seus elementos? E se ele não existe, que significado têm os números que encontramos?
  • Todos chegaríamos aos mesmos números?



E existe um hipertetraedro (4D)?
Por favor habilite Java para uma construção interativa (com Cinderella).
A projecção (paralela) de um triângulo sobre uma recta
é um segmento com um ponto no meio.
Um triângulo tem 3 vértices, 3 arestas e uma face 2D.
Por favor habilite Java para uma construção interativa (com Cinderella).
A projecção (paralela) de um tetraedro sobre um plano
é um triângulo com um ponto no meio.
Um tetraedro tem 4 vértices, 6 arestas, 4 faces 2D e uma face 3D.

Por favor habilite Java para uma construção interativa (com Cinderella).


A projecção (paralela) de um hipertetradedro 4D sobre o espaço
é um tetraedro 3D com um ponto no meio.

Quantos vértices, arestas, faces 2D, faces 3D e faces 4D tem um hipertetradedro?

E quanto aos outros sólidos Platónicos? Quais são os seus análogos quadrimensionais?
E em dimensões mais altas, o que acontece?