A Fórmula de Euler
João Nuno Tavares
I. PROVA

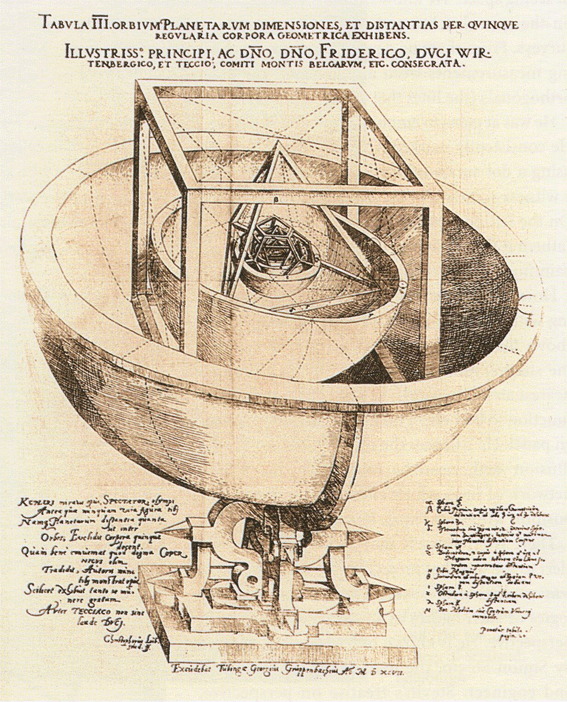
Modelos de pedra do cubo, tetraedro, dodecaedro, icosaedro e octaedro, feitos no
período neolítico (cerca de 2000 a.C.)
 Sólidos Platónicos |
 |
|
|
|
|
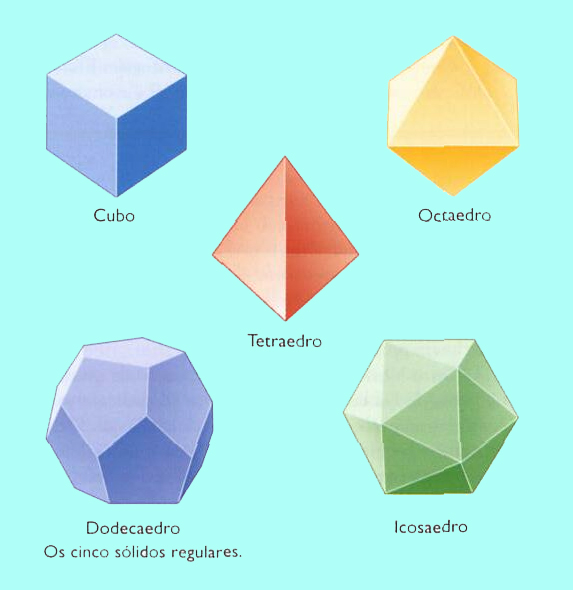 |
 O que é a dualidade? |
| V (vértices) |
A (arestas) | F (faces) | V-A+F=X(S) |
|
| Octaedro | 6 |
12 | 8 | 2 |
| Cubo | 8 | 12 | 6 | 2 |
| Tetraedro | 4 | 6 | 4 | 2 |
| Dodecaedro | 20 | 30 | 12 | 2 |
| Icosaedro | 12 | 30 | 20 | 2 |
Prova de Cauchy
da fórmula de Euler
V-A+F=2
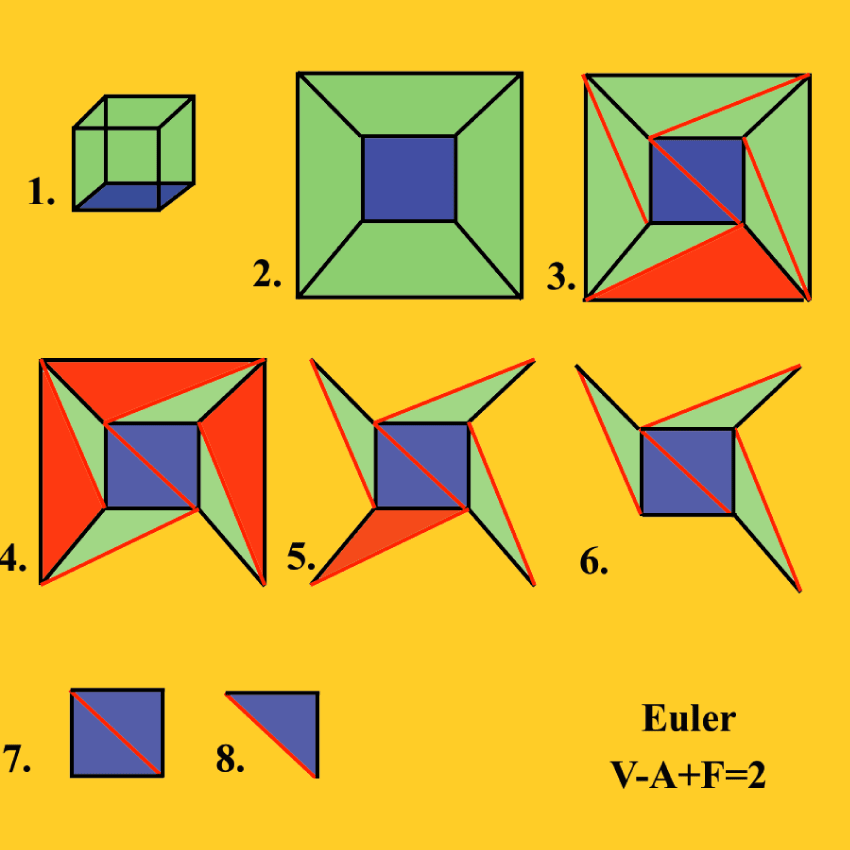
| Prova de Cauchy da fórmula de Euler V-A+F=2 |
||
V - A + F = 1
|
||
|
||
V - (A - 1) + (F - 1) = V - A + F
a soma V - A + F mantem-se inalterada. |
||
(V - 1) - (A - 2) + (F - 1) = V - A + F
a soma V - A + F mantem-se mais uma vez inalterada. |
||
V - A + F = 3 - 3 + 1 = 1
o que termina a demonstração.
|
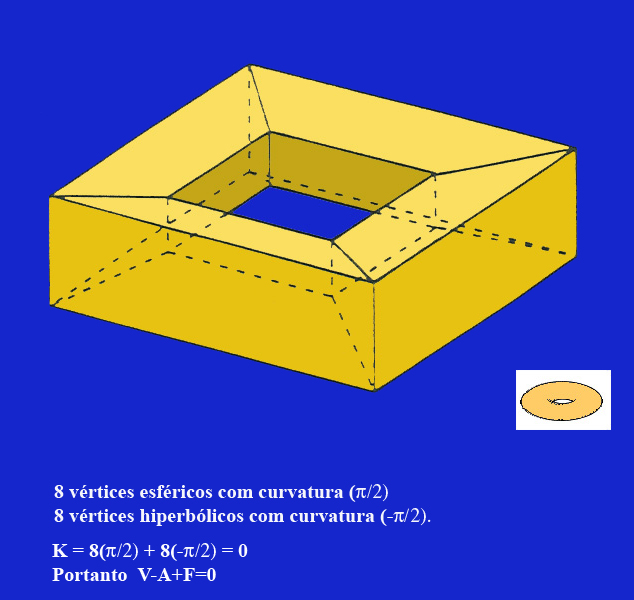
II. Refutação
| A fórmula de Euler não
é válida para superfícies poliedrais com buracos! Por exemplo: |
 V-A+F = 16-32+16 = 0 |
 V-A+F = 28-62+32 = - 2 |
Definamos a curvatura de Gauss K(v),
de cada
vértice v do poliedro,
através de: Existem três tipos de vértices:
 |
Teorema
de Descartes-Gauss-Bonnet
 onde K = Curvatura total = Soma das curvaturas K(v) |
Exemplos
 |
 |
Demonstração do Teorema de Descartes-Gauss-Bonnet
µ


A soma dos ângulos externos de um polígono convexo é igual a 2pi.
A soma dos ângulos internos de um polígono convexo com n lados é igual a (n-2)pi.