



Recorde que um dos princípios em que se baseia a teoria da Relatividade Restritaé o chamado:
Princípio da relatividade [Galileu] ... Dois observadores que se movem com velocidade uniforme, um relativamente ao outro, devem formular as leis da natureza exactamente da mesma forma. Em particular, nenhum observador de inércia pode distinguir entre repouso absoluto e movimento absoluto, com apelo exclusivo às leis da natureza. Não existe pois movimento absoluto, mas apenas movimento relativo (de um observador relativamente a um outro).
Portanto, os referenciais de inércia têm um estatuto
especial em Relatividade Restrita. Todos os
referenciais de inércia movem-se com velocidade uniforme uns
relativamente aos
outros. Se ![]() é um referencial de inércia e se
é um referencial de inércia e se ![]() acelera relativamente a
acelera relativamente a
![]() (a velocidade de
(a velocidade de ![]() , relativa a
, relativa a ![]() , varia), então
, varia), então
![]() não é um referencial de inércia.
não é um referencial de inércia.
As leis da Física são mais
complicadas em ![]() . Observadores em
. Observadores em ![]() sentem forças
fictícias, ditas forças de inércia, que,
numa primeira
análise, não podem ser atribuídas a qualquer
agente directo.
Num referencial acelerado
sentem forças
fictícias, ditas forças de inércia, que,
numa primeira
análise, não podem ser atribuídas a qualquer
agente directo.
Num referencial acelerado ![]() , a lei de inércia não é válida -
a velocidade de um corpo varia embora não haja qualquer
"força
real" que sobre ele actua!
, a lei de inércia não é válida -
a velocidade de um corpo varia embora não haja qualquer
"força
real" que sobre ele actua!
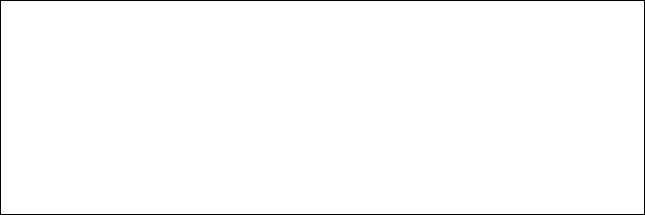 |
Vejamos um exemplo concreto:
num referencial não
inercial ![]() , que se move com aceleraçãolinear constante e
igual a
, que se move com aceleraçãolinear constante e
igual a ![]() , relativamente a um referencial de inércia
, relativamente a um referencial de inércia ![]() .
.
Suponhamos que o movimento se faz ao longo do eixo dos ![]() e que os
restantes eixos se mantêm sempre paralelos. A
relação entre as
coordenadas dos dois referenciais é dada por:
e que os
restantes eixos se mantêm sempre paralelos. A
relação entre as
coordenadas dos dois referenciais é dada por:
APPLETT (ja esta feito)
Derivando duas vezes relativamente a ![]() (ou
(ou ![]() ), obtemos:
), obtemos:
Suponhamos que uma partícula, de massa ![]() , se move ao longo do eixo
dos
, se move ao longo do eixo
dos ![]() , sob influência de uma força constante
, sob influência de uma força constante ![]() . A
segunda lei de Newton, em
. A
segunda lei de Newton, em ![]() , é:
, é:
Portanto, num referencial não inercial, os corpos estão sujeitos a pseudo-forças (forças de inércia) que, em princípio, não podem ser atribuídas a qualquer agente directo (figura 1).
Em Relatividade Restrita postula-se que as leis da Física devem ter a mesma forma em todos os referenciais de inércia. Estes referenciais desempenham pois um papel privilegiado relativamente a referenciais acelerados. No entanto, este estatuto especial dos referenciais de inércia era contrário à visão que Einstein tinha da realidade! Porque motivo a Natureza atribuiria um papel de privilégio aos referenciais de inércia? O facto de estar em movimento uniforme depende aliás do estado de movimento de quem observa.
As leis da Física devem pois poder exprimir-se sob a mesma
forma não importa qual o tipo de referencial. Nas
próprias palavras de
Einstein: "Que é que a Natureza tem a ver com os sistemas
de coordenadas e respectivos estados de movimento? Afinal não
sômos nós que os introduzimos para descrever
matematicamente os
fenómenos?".
Na sua teoria da Relatividade Geral, Einstein generaliza o Princípio da Relatividade de Galileu, enunciando o seu:
Princípio da Relatividade Geral [Einstein] ... Todos os referenciais, qualquer que seja o seu estado de movimento, devem ser equivalentes para exprimir as leis da Natureza.
É claro que esta é uma ideia completamente revolucionária, que parece contrariar algumas observações familiares. Quando estamos num carro que acelera somos empurrados para trás (figura 1). Parece difícil admitir que as leis da mecânica são as mesmas num referencial de inércia e num referencial acelerado.
Duas questões ainda:
Newton responde postulando a existência de um espaço absoluto - um espaço que existe independentemente de tudo, imutável, um palco absoluto no qual se desenrolam os acontecimentos naturais. Um observador inercial é pois, segundo Newton, aquele que está em repouso ou em movimento uniforme relativamente ao espaço absoluto. As forças de inércia ocorrem apenas para aqueles observadores que têm uma aceleração absoluta relativamente ao espaço absoluto.
A experiência do balde de água, que descrevemos na secção seguinte, determina, segundo Newton, quando um sistema está em rotação absoluta relativamente ao espaço absoluto.
Imaginemos um balde, quase cheio com água, suspenso por uma corda, em torno da qual roda (figura 2):
 |
Como é familiar, no início o balde roda e a
superfície da
água mantem-se plana. Porém, gradualmente, a água
vai rodando
e a sua superfície deforma-se, elevando-se no bordo, adquirindo
uma forma côncava, devido à força
centrífuga. Se,
subitamente, paramos o balde, a água continua a rodar e a sua
superfície mantem a forma côncava (figura 2).
Mais esquematicamente:
Newton diz que a curvatura da superfície da água em A2. e A3. se deve à força centrífuga, resultante da rotação da água, relativamente ao espaço absoluto. Esta curvatura não se deve a efeitos locais como, por exemplo, a rotação do balde. De facto, em A1. a superfície da água é plana, embora o balde rode, enquanto que em A3., a superfície da água é côncava, embora o balde esteja parado.
Newton explica pois a deformação da superfície da água, atribuindo-a à força centrífuga que se desenvolve relativamente ao espaço absoluto. No entanto, diz Einstein, o espaço absoluto é uma pura abstracção, não é observável, e fica por explicar a verdadeira causa da elevação da água no bordo.
Mach atribui esta elevação à presença das outras massas do universo. A água roda, não apenas relativamente ao balde, mas também relativamente a todas as outras massas - estas podem, por isso, ser consideradas como a causa da força centrífuga.
A força centrífuga não indica pois rotação relativamente ao espaço absoluto, mas sim rotação relativamente às massas do universo.
Do ponto de vista do balde e da água é todo o universo que roda! De acordo com Mach, a força centrífuga é pois um efeito gravitacional dinâmico das massas que rodam.
Um observador que vê um objecto mover-se segundo uma trajectória curvílinea (não rectilínea) dirá que isso acontece porque, de acordo com a lei de Newton, existe uma força que actua sobre esse objecto.
Suponhamos, no entanto, que um outro observadorolha para o mesmo objecto e vê que este se desloca segundo uma trajectória rectilínea, com velocidade uniforme, e que, portanto, novamente de acordo com a lei de Newton, não está sujeito à acção de qualquer força.
Será isto possível? E quem tem razão? Será possível que dois observadores distintos possam discordar àcerca (i). da trajectória ser rectilínea ou curvílinea e (ii). àcerca do facto do objecto estar ou não sujeito à acção de uma força exterior?
Vejamos um exemplo concreto:
Suponhamos que o movimento se faz ao longo do eixo dos ![]() e que os
restantes eixos se mantêm sempre paralelos. A
relação entre as
coordenadas dos dois referenciais é dada por:
e que os
restantes eixos se mantêm sempre paralelos. A
relação entre as
coordenadas dos dois referenciais é dada por:
APPLETT Cinderella
Supômos que não há efeitos relativistas, de
tal forma que,
![]() . Consideremos agora uma partícula livre
(ou um raio de luz)
que se move com velocidade constante
. Consideremos agora uma partícula livre
(ou um raio de luz)
que se move com velocidade constante ![]() , no plano
, no plano ![]() ,
paralelamente ao eixo dos
,
paralelamente ao eixo dos ![]() no referencial de
inércia
no referencial de
inércia ![]() .
.
De facto:
Portanto, quando obervada no referencial
![]() , a partícula segue uma
trajectória parabólica
, a partícula segue uma
trajectória parabólica
Suponhamos que um astronauta ![]() está numa cápsula espacial,
várias dezenas de kms acima da superfície terrestre, em
queda
livre. Um observador
está numa cápsula espacial,
várias dezenas de kms acima da superfície terrestre, em
queda
livre. Um observador ![]() está em terra e vê o
comportamento
de
está em terra e vê o
comportamento
de ![]() através de um telescópio.
através de um telescópio.
 |
![]() está em repouso na superfície da
terra, e vê
está em repouso na superfície da
terra, e vê ![]() cair verticalmente
com uma aceleração de
cair verticalmente
com uma aceleração de ![]() . Tudo o que está na cápsula
espacial comporta-se da mesma forma - tudo cai com a mesma
aceleração. Se, por exemplo,
. Tudo o que está na cápsula
espacial comporta-se da mesma forma - tudo cai com a mesma
aceleração. Se, por exemplo, ![]() atira uma bola para o lado,
atira uma bola para o lado,
![]() verá a bola descrever uma parábola, como acontece com
qualquer projéctil.
verá a bola descrever uma parábola, como acontece com
qualquer projéctil.
Consideremos agora as sensações do astronauta ![]() . Se ele
quiser pôr um quadro na parede da cápsula, basta
encostá-lo,
não precisa de o pregar!
. Se ele
quiser pôr um quadro na parede da cápsula, basta
encostá-lo,
não precisa de o pregar! ![]() compreende que assim é, porque
ele vê que a parede e o quadro caiem ambos com a mesma
aceleração.
compreende que assim é, porque
ele vê que a parede e o quadro caiem ambos com a mesma
aceleração. ![]() larga uma maçã que tem na
mão e vê
que ela permanece suspensa no ar.
larga uma maçã que tem na
mão e vê
que ela permanece suspensa no ar. ![]() dirá que
dirá que ![]() e a maçã caiem lado a lado.
Quando
e a maçã caiem lado a lado.
Quando ![]() atira uma bola, ele verá a
bola deslocar-se em linha recta até colidir com a parede da
cápsula, embora
atira uma bola, ele verá a
bola deslocar-se em linha recta até colidir com a parede da
cápsula, embora ![]() veja a bola descrever uma parábola.
veja a bola descrever uma parábola.
![]() pesa-se numa balança a bordo e vê que o seu
peso é
zero!
pesa-se numa balança a bordo e vê que o seu
peso é
zero!
Todas estas experiências convencem o astronauta ![]() de
que ele está em repouso, num espaço livre de qualquer
atracção gravitacional, enquanto que
de
que ele está em repouso, num espaço livre de qualquer
atracção gravitacional, enquanto que ![]() continua convencido
que
continua convencido
que ![]() cai num campo de forças uniforme.
cai num campo de forças uniforme.
Para reconciliar estes dois pontos de vista, ![]() escolhe um
referencial ligado à cápsula, enquanto que
escolhe um
referencial ligado à cápsula, enquanto que ![]() escolhe um referencial
ligado à terra. Estes dois referenciais movem-se um
relativamente ao
outro com aceleraçãolinear constante. As
consequências
imediatas deste facto são (i). aquilo a que
escolhe um referencial
ligado à terra. Estes dois referenciais movem-se um
relativamente ao
outro com aceleraçãolinear constante. As
consequências
imediatas deste facto são (i). aquilo a que ![]() chama uma
recta,
chama uma
recta, ![]() dirá que é uma curva, (ii). uma região que
dirá que é uma curva, (ii). uma região que ![]() declara que está livre de qualquer
atracção
gravitacional,
declara que está livre de qualquer
atracção
gravitacional, ![]() dirá que está sujeita a um campo
gravitacional uniforme. Esta relação é
recíproca -
dirá que está sujeita a um campo
gravitacional uniforme. Esta relação é
recíproca - ![]() dirá que a terra e
dirá que a terra e ![]() se deslocam com aceleração
uniforme na
sua direcção.
se deslocam com aceleração
uniforme na
sua direcção.
Como vimos, a teoria da Relatividade Geral proíbe que privilegiemos qualquer observador relativamente a qualquer outro. Não pode haver qualquer tipo de favoritismo. Qualquer lei da Natureza é igualmente aceitável para todos os observadores e deve por isso ter uma forma invariante que sobreviva à mudança de coordenadas correspondentes. Em particular, a situação acima descrita mostra que a força gravitacional é uma ilusão - depende do referencial escolhido. Isto não significa que se nos lançarmos do cimo de uma torre não haja consequências desastrosas! Mas Einstein nega que elas se devem à atracção que a terra exerce sobre nós! Veremos em breve qual a explicação de Einstein.
No exemplo acima, consideramos o efeito da
gravitaçãoapenas
numa pequena região que, de acordo com Newton, está
sujeita à
acção de uma campo uniforme. Vimos que, nesta
situação, todos os
seus efeitos podem ser neutralizados por uma mudança de
referencial. A existência de um campo gravitacional uniforme, de
acordo
com ![]() , é negada pelo astronauta
, é negada pelo astronauta ![]() que escolhe um referencial
que se move com aceleração constante relativamente a
que escolhe um referencial
que se move com aceleração constante relativamente a ![]() . Um
outro observador ligado ao seu referencial afirmará porventura a
existência
de um outro tipo de campo.
. Um
outro observador ligado ao seu referencial afirmará porventura a
existência
de um outro tipo de campo.
Uma escolha conveniente de referencial neutralizará qualquer campo gravitacional uniforme. Portanto, um campo deste tipo é artificial, uma pura invenção do observador, e não uma propriedade intrínseca da Natureza...
O astronauta ![]() , ao escolher um referencial apropriado, neutralizou, na
sua
vizinhança imediata, aquilo a que
, ao escolher um referencial apropriado, neutralizou, na
sua
vizinhança imediata, aquilo a que ![]() chama um campo
gravitacional (figura 3). No entanto, ao
fazê-lo,
chama um campo
gravitacional (figura 3). No entanto, ao
fazê-lo, ![]() vê agora
vê agora ![]() a deslocar-se na sua
direcção com aceleração
a deslocar-se na sua
direcção com aceleração ![]() . Portanto agora
. Portanto agora ![]() diz que
diz que ![]() está num campo de forças. Embora a escolha do
referencial feita por
está num campo de forças. Embora a escolha do
referencial feita por ![]() neutralize o efeito da gravidade, na sua
vizinhança imediata, ele piora a situação noutros
lugares,
criando outros campos com outras grandezas e direcções.
neutralize o efeito da gravidade, na sua
vizinhança imediata, ele piora a situação noutros
lugares,
criando outros campos com outras grandezas e direcções.
Princípio da Equivalência [Einstein] ... "Se nos restringirmos a uma pequena região do espaço, um campo de gravitação uniforme é equivalente a um referencial que se move com aceleraçãolinear constante, num campo livre de gravidade. Não é possível distinguir as duas situações por qualquer experiência" (figura 4).
Outras formulações:
Física num referencial em queda livre num campo gravitacional uniforme é equivalente à Física num referencial de inércia sem gravidade
Por outras palavras, dentro de um referencial em queda livre, onde a aceleração cancela exactamente o campo gravitacional uniforme, não é possível detectar nem da aceleração nem a gravidade através de qualquer experiência.
A Física num referencial não acelerado num campo
gravitacional ![]() é
equivalente à Física num referencial sem gravidade mas
com
aceleração
é
equivalente à Física num referencial sem gravidade mas
com
aceleração ![]() .
.
Portanto, de acordo com o Princípio de Equivalência, referenciais acelerados podem ser tratados da mesma forma que os referenciais de inércia- eles não são mais do que referenciais de inércia com gravidade. Daqui resulta também uma definição física de referencial de inércia, sem qualquer referência a algo de exterior como, por exemplo, estrelas fixas - um referencial de inércia é apenas um referencial sem gravidade.
Vejamos mais um exemplo sugestivo. Consideremos as seguintes situações locais:
 |
 |
 |
 |
Claramente que, do ponto de vista do astronauta, dentro da caixa, as situações S 1 e S 3 são indistinguíveis, bem como as situações S 2 e S 4, de acordo com o Princípio de Equivalência.
Consideremos um sistema de partículas com massas
![]() , interagindo umas com as outras de tal forma
que cada uma delas exerce uma força sobre cada uma das
restantes.
, interagindo umas com as outras de tal forma
que cada uma delas exerce uma força sobre cada uma das
restantes.
Para ![]() , seja
, seja ![]() a força que a partícula
a força que a partícula ![]() exerce sobre a partícula
exerce sobre a partícula ![]() . Por simplicidade, supômos que (i).
a força está dirigida segundo a linha que une as
partículas
. Por simplicidade, supômos que (i).
a força está dirigida segundo a linha que une as
partículas
![]() e
e ![]() , (ii). é uma função apenas da distância
entre elas,
e (iii).
, (ii). é uma função apenas da distância
entre elas,
e (iii). ![]() ,
, ![]() .
.
Um observador ![]() ligado ao referencial
ligado ao referencial ![]() usa coordenadas
usa coordenadas
![]() para acontecimentos, enquanto que um
observador
para acontecimentos, enquanto que um
observador ![]() , ligado ao
referencial
, ligado ao
referencial ![]() , usa coordenadas
, usa coordenadas ![]() para esses mesmos
acontecimentos. Supômos ainda que as velocidades envolvidas
são
suficientemente pequenas para que seja possível uma
análise
não relativista. Pômos portanto
para esses mesmos
acontecimentos. Supômos ainda que as velocidades envolvidas
são
suficientemente pequenas para que seja possível uma
análise
não relativista. Pômos portanto ![]() e
usamos a notação:
e
usamos a notação:
Sejam ![]() e
e ![]() , os vectores de posição da partícula
, os vectores de posição da partícula
![]() ,
, ![]() , relativamente aos referenciais
, relativamente aos referenciais ![]() e
e ![]() ,
respectivamente.
,
respectivamente.
Se o primeiro observador ![]() acredita que está na presença
de um campo gravitacional uniforme, de tal forma que, relativamente
a ele, todas as partículas livres caiem com a mesma
aceleração,
dada por um vector constante
acredita que está na presença
de um campo gravitacional uniforme, de tal forma que, relativamente
a ele, todas as partículas livres caiem com a mesma
aceleração,
dada por um vector constante ![]() , então as equações do
movimento são, para esse observador:
, então as equações do
movimento são, para esse observador:
Suponhamos que a aceleração relativa entre os dois
referenciais, ![]() e
e ![]() , é constante em grandeza e direcção. Mais
concretamente:
, é constante em grandeza e direcção. Mais
concretamente:
Substituindo, para cada ![]() , a equação (10) em
(8), obtemos as seguintes equações do
movimento,
descritas agora no referencial
, a equação (10) em
(8), obtemos as seguintes equações do
movimento,
descritas agora no referencial ![]() , i.e., relativas ao segundo
observador
, i.e., relativas ao segundo
observador ![]() :
:
Nota: como ![]() é apenas função de
é apenas função de
![]() , e como
, e como ![]() ,
, ![]() é o mesmo em ambos os referenciais.
é o mesmo em ambos os referenciais.
Conclusão: O campo gravitacional foi cancelado
no referencial ![]() . Para o observador
. Para o observador ![]() não existe campo
gravitacional. O observador
não existe campo
gravitacional. O observador ![]() interpreta isto dizendo que
interpreta isto dizendo que ![]() está em queda livre e que por isso não sente campo
gravitacional. Por outro lado,
está em queda livre e que por isso não sente campo
gravitacional. Por outro lado, ![]() poderá dizer: "Não, meu
caro! De facto não existe campo gravitacional. Eu sou um
observador
inercial e você sente campo gravitacional apenas pelo facto de
que
você acelera relativamente a mim!"
poderá dizer: "Não, meu
caro! De facto não existe campo gravitacional. Eu sou um
observador
inercial e você sente campo gravitacional apenas pelo facto de
que
você acelera relativamente a mim!"
A massa de inércia, ![]() , de um corpo é uma medida da sua inércia, isto é,
da resistência que ele
oferece à mudança do seu movimento. É a massa que
surge na
primeira equação de Newton:
, de um corpo é uma medida da sua inércia, isto é,
da resistência que ele
oferece à mudança do seu movimento. É a massa que
surge na
primeira equação de Newton:
Se o corpo está sob a acção de um campo
gravitacional,
criado por um outro corpo esférico de massa (gravitacional) ![]() (uma estrela, por exemplo), cujo centro está a uma
distância
(uma estrela, por exemplo), cujo centro está a uma
distância ![]() do primeiro, a força gravitacional,
do primeiro, a força gravitacional, ![]() , que actua sobre
o primeiro corpo, é determinada pela sua massa
gravitacional,
, que actua sobre
o primeiro corpo, é determinada pela sua massa
gravitacional, ![]() , e é dada pela lei de atracção
universal de Newton:
, e é dada pela lei de atracção
universal de Newton:
APPLETT AtracaoUniversal.html
Portanto, a massa gravitacional mede a resposta de um objecto à atracção gravitacional. Podemos ver estas massas gravitacionais como fontes que geram força gravitacional, ou ainda como "cargas" gravitacionais que se atraiem uma à outra.
A massa de inércia ![]() e a massa
gravitacional
e a massa
gravitacional ![]() de um
corpo, podem, à priori, ser diferentes e variar com a
substância
de que ele é feito.
de um
corpo, podem, à priori, ser diferentes e variar com a
substância
de que ele é feito.
Para comparar estas duas noções de massa, consideremos
como a
gravidade terrestre actua sobre um corpo situado à
superfície da
terra. Neste caso, ![]() será igual à
distância entre o corpo e
o centro da terra e
será igual à
distância entre o corpo e
o centro da terra e ![]() a massa gravitacional da terra.
a massa gravitacional da terra.
![]() e
e ![]() são pois constantes. A
força gravitacional
são pois constantes. A
força gravitacional ![]() ,
dada por (13), que actua sobre o corpo, é
portanto
proporcional à sua massa gravitacional
,
dada por (13), que actua sobre o corpo, é
portanto
proporcional à sua massa gravitacional ![]() :
:
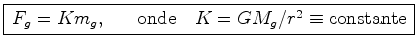 |
(14) |
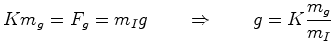 |
(15) |
Se existissem dois corpos para os quais ![]() fossem diferentes,
então
fossem diferentes,
então ![]() também seria e os tais dois corpos
caíriam com
acelerações distintas. Mas isso nunca foi observado!
Aliás, é célebre a experiência realizada por
Galileu no cimo da torre de Pisa
(figura 9)!
também seria e os tais dois corpos
caíriam com
acelerações distintas. Mas isso nunca foi observado!
Aliás, é célebre a experiência realizada por
Galileu no cimo da torre de Pisa
(figura 9)!
Newton postulou que a razão, ![]() , entre as duas massas
de um mesmo corpo, é independente da substância de que ele
é
feito. Escolhendo convenientemente as unidades podemos até
supôr que:
, entre as duas massas
de um mesmo corpo, é independente da substância de que ele
é
feito. Escolhendo convenientemente as unidades podemos até
supôr que:
A queda livre de corpos no vazio suporta experimentalmente este
postulado - todos os corpos caiem com a mesma aceleração
num
campo gravitacional dado.
A lei de atracção universal confere pois à
força de
atracção gravitacional uma característica
única
entre todas as forças conhecidas na Natureza. Com efeito, a
aceleração, ![]() , comunicada a uma massa
, comunicada a uma massa ![]() por uma força
qualquer
por uma força
qualquer ![]() , depende da sua massa, uma vez que
, depende da sua massa, uma vez que ![]() . Pelo
contrário, um corpo colocado num campo gravitacional criado por
uma massa
. Pelo
contrário, um corpo colocado num campo gravitacional criado por
uma massa ![]() , adquire uma aceleração independente da sua
massa, já que
, adquire uma aceleração independente da sua
massa, já que ![]() e, portanto,
e, portanto, ![]() .
.
A aceleração da gravidade é portanto a mesma para todos os corpos - a força gravitacional ajusta-se de alguma forma à massa de cada corpo sobre o qual actua, de tal forma que a todos imprime a mesma aceleração! É esta aliás a propriedade notável do campo gravitacional, que torna possível criá-lo artificialmente.
Corpos em queda livre, isto é, sujeitos apenas à acção da gravidade, caiem lado a lado, todos com a mesma aceleração.
Mas, como já vimos na secção anterior, podemos
simular exactamente a mesma situação, por exemplo, no
interior de uma nave, fora da influência de qualquer campo
gravitacional, cujos motores a impulsionam numa direcção
fixa com uma aceleração constante. Corpos em queda livre
dentro da nave sofrem todos uma mesma aceleração na
direcção oposta. Portanto, num referencial ligado
à nave, criámos um campo gravitacional.
Podemos até neutralizar um campo gravitacional. Isto é
o que acontece nos aviões ![]() , usados em experiências para testar ausência de peso. De
20 em 20 segundos, eles voam como um projéctil que é
disparado para cima e depois cai sob a acção da gravidade
terrestre. Dentro do avião, objectos que se movem livremente,
caiem exactamente como o avião, à mesma razão.
Portanto, relativamente a um referencial ligado ao avião, eles
exibem aceleração nula. Eles flutuam. A gravidade
terrestre foi cancelada ou neutralizada e atinge-se o ponto
, usados em experiências para testar ausência de peso. De
20 em 20 segundos, eles voam como um projéctil que é
disparado para cima e depois cai sob a acção da gravidade
terrestre. Dentro do avião, objectos que se movem livremente,
caiem exactamente como o avião, à mesma razão.
Portanto, relativamente a um referencial ligado ao avião, eles
exibem aceleração nula. Eles flutuam. A gravidade
terrestre foi cancelada ou neutralizada e atinge-se o ponto ![]() .
.
Mas regressemos ao Princípio da Equivalência de Newton:
![]() . Como explicar esta igualdade entre massa de inércia
. Como explicar esta igualdade entre massa de inércia ![]() e a
massa gravitacional
e a
massa gravitacional ![]() ? Newton constatou um facto experimental
e, de seguida, elevou-o à categoria de postulado. Mas não
deu
uma explicação para isso!
? Newton constatou um facto experimental
e, de seguida, elevou-o à categoria de postulado. Mas não
deu
uma explicação para isso!
A explicação de Einstein está no seu:
Princípio da Equivalência ... Um campo de gravitação é localmente equivalente a um campo de aceleração. Um referencial acelerado e um campo de gravitação, que aponta na direcção contrária à da aceleração, são equivalentes. Não existe maneira de distinguir as duas situações!
Imaginemos um corpo de massa ![]() suspenso por uma
mola, presa à
parte superior de uma caixa (um elevador, por exemplo). Um observador
dentro da caixa vê subitamente a mola alongar-se. O
acréscimo da tensão da mola indica que o corpo foi puxado
(figura 10).
suspenso por uma
mola, presa à
parte superior de uma caixa (um elevador, por exemplo). Um observador
dentro da caixa vê subitamente a mola alongar-se. O
acréscimo da tensão da mola indica que o corpo foi puxado
(figura 10).
Existem duas explicações possíveis:
Os efeitos de um campo gravitacional e de um campo de
aceleração são pois os
mesmos e um observador, situado no interior da caixa, não tem
maneira de
distinguir entre as duas situações acima descritas. Em E1.
(campo gravitacional), o
alongamento da mola é determinado pela massa gravitacional ![]() do corpo. Por outro lado, em E2. (campo de
aceleração), esse mesmo
alongamento é determinado pela sua massa de inércia
do corpo. Por outro lado, em E2. (campo de
aceleração), esse mesmo
alongamento é determinado pela sua massa de inércia ![]() . Como
o alongamento nos dois casos é o mesmo, sômos levados a
concluir
que
. Como
o alongamento nos dois casos é o mesmo, sômos levados a
concluir
que ![]() . E isto acontece qualquer que seja o corpo.
É esta a explicação dada por Einstein para a
igualdade
. E isto acontece qualquer que seja o corpo.
É esta a explicação dada por Einstein para a
igualdade ![]() !
!
Em 1911 Einstein deduziu várias consequências do seu Princípio de Equivalência.
Considere a seguinte experiência conceptual: luz de
frequência
![]() é emitida do chão de uma nave de altura
é emitida do chão de uma nave de altura ![]() , que se move com
uma aceleração linear constante
, que se move com
uma aceleração linear constante ![]() , dirigida para cima, no
espaço exterior, longe de qualquer campo gravitacional.
, dirigida para cima, no
espaço exterior, longe de qualquer campo gravitacional.
A luz é detectada por um receptor, estacionado no topo da nave. Que frequência é que ele mede ?
Note que o receptor não é um observador de inércia. Como podemos pois dizer algo àcerca das suas medições? Einstein assumiu a hipótese, válida em primeira aproximação para acelerações fracas, que toda a medição feita por um observador acelerado é a mesma da que é obtida por um observador de inércia, que tem a mesma velocidade no instante e local em que é feita a medição.
Sendo assim, seja ![]() um referencial de inércia no qual o
emissor está
momentâneamente em repouso, no instante em que emite o raio
luminoso, e
um referencial de inércia no qual o
emissor está
momentâneamente em repouso, no instante em que emite o raio
luminoso, e ![]() um referencial de inércia no qual o receptor
está em repouso
quando a luz é detectada.
um referencial de inércia no qual o receptor
está em repouso
quando a luz é detectada.
É claro que emissor e receptor afastam-se um do outro.
Portanto,
de acordo com a teoria do efeito Doppler, a frequência ![]() ,
medida pelo receptor, é inferior a
,
medida pelo receptor, é inferior a ![]() . O receptor detecta pois um
desvio para o vermelho (redshift). Como se viu antes:
. O receptor detecta pois um
desvio para o vermelho (redshift). Como se viu antes:
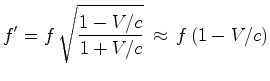 |
(17) |
De acordo com o Princípio de Equivalência, o mesmo efeito deve ser observado se o elevador, em vez de estar acelerado, está sob a acção de um campo gravitacional dirigido para baixo. Como o receptor está, neste caso, sempre em repouso relativamente ao emissor, ele não pode atribuir o reshift ao efeito Doppler. Deve sim interpretá-lo como um efeito da gravidade.
Concluímos pois que a luz sofre um desvio para o vermelho quando se move na direcção contrária à de um campo gravitacional. Luz que se move na direcçãode um campo gravitacional sofre um desvio para o azul.
Vamos comparar dois relógios ![]() e
e ![]() , o primeiro colocado no
topo e o segundo na base de um foguetão, quando este acelera
para cima (figura 11). Vamos ver que, para um
astronauta
sentado na base do foguetão, o relógio
, o primeiro colocado no
topo e o segundo na base de um foguetão, quando este acelera
para cima (figura 11). Vamos ver que, para um
astronauta
sentado na base do foguetão, o relógio ![]() parece andar mais
depressa do que o relógio
parece andar mais
depressa do que o relógio ![]() .
.

Figura:
Para ver isto, imaginemos que o relógio ![]() emite um
pulso de
luz por segundo, e suponhamos que o nosso astronauta está na
base
do foguetão a comparar os instantes de chegada desses sucessivos
pulsos com os tics do seu relógio
emite um
pulso de
luz por segundo, e suponhamos que o nosso astronauta está na
base
do foguetão a comparar os instantes de chegada desses sucessivos
pulsos com os tics do seu relógio ![]() .
.
No instante 0
, o relógio ![]() emite o primeiro pulso em
direcção a
emite o primeiro pulso em
direcção a ![]() . Entretanto o foguetão sobe um pouco, e esse
pulso, depois de percorrer uma distância
. Entretanto o foguetão sobe um pouco, e esse
pulso, depois de percorrer uma distância ![]() , atinge
, atinge ![]() , quando
este está na posição
, quando
este está na posição ![]() (figura 11).
(figura 11).
No segundo seguinte, ![]() , que agora ocupa a posição
, que agora ocupa a posição![]() emite o
próximo pulso em direcção a
emite o
próximo pulso em direcção a ![]() . O foguetão sobe mais ainda,
e este segundo pulso, depois de percorrer uma distância
. O foguetão sobe mais ainda,
e este segundo pulso, depois de percorrer uma distância ![]() ,
atinge
,
atinge ![]() , quando este está na posição
, quando este está na posição ![]() (figura
11).
(figura
11).
É claro que ![]() , uma vez que o foguetão acelera e tem por
isso mais velocidade no instante da emissão do segundo pulso.
, uma vez que o foguetão acelera e tem por
isso mais velocidade no instante da emissão do segundo pulso.
Portanto se os dois pulsos foram emitidos por ![]() , separados por um
intervalo de tempo de
, separados por um
intervalo de tempo de ![]() segundo, eles chegam a
segundo, eles chegam a ![]() com um
intervalo ligeiramente inferior a
com um
intervalo ligeiramente inferior a ![]() segundo, já
que o segundo
pulso não demora tanto tempo na viagem. O mesmo acontece para
todos os pulsos seguintes.
segundo, já
que o segundo
pulso não demora tanto tempo na viagem. O mesmo acontece para
todos os pulsos seguintes.
Portanto o astronauta na base do foguetão, junto de ![]() ,
concluirá que o relógio
,
concluirá que o relógio ![]() anda mais depressa
do que o
relógio
anda mais depressa
do que o
relógio ![]() .
.
Se o astronauta estivesse no nariz do foguetão, observando
agora, junto de ![]() , pulsos emitidos de
, pulsos emitidos de ![]() , ele concluiria que o relógio
, ele concluiria que o relógio ![]() anda mais devagar do
que
anda mais devagar do
que ![]() .
.
Pelo Princípio de Equivalência, o mesmo se passa quando
o foguetão está estacionado à superfície da
Terra, sujeito pois ao campo gravitacional terrestre.
Como neste caso, ![]() está mais perto do corpo
gravitacional do que
está mais perto do corpo
gravitacional do que
![]() , concluímos que:
, concluímos que:
relógios mais próximos de um corpo massivo andam mais
devagar do que os relógios mais afastados.
Este fenómeno da dilatação gravitacional do tempo complica a atribuição de coordenadas temporais a acontecimentos, na presença de um campo gravitacional. De facto, em Relatividade Restrita, a coordenada temporal de um acontecimento, num dado referencial de inércia, define-se pela leitura de um relógio em repouso relativamente a esse referencial, e situado no mesmo local desse acontecimento. Como temos a possibilidade de sincronizar todos os relógios num dado referencial de inércia, este processo atribui de forma unívoca um valor para a coordenada temporal de cada acontecimento.
Mas, num campo gravitacional, os relógios em diferentes locais marcam o tempo de forma diferente, i.e., os tics dos relógios são diferentes conforme o local onde eles se encontram. Portanto eles não podem ser sincronizados. Como podemos então comparar as coordenadas temporais de acontecimentos que ocorrem em locais distintos ?
Suponhamos que se pretende fazer um rectângulo no
espaço-tempo. Começamos por usar um diagrama "altura ![]() versus tempo
versus tempo ![]() ". Como base
do nosso rectângulo tomamos um objecto
". Como base
do nosso rectângulo tomamos um objecto ![]() em
repouso, situado
à altura
em
repouso, situado
à altura ![]() , e seguimos a sua linha de universo durante
, e seguimos a sua linha de universo durante ![]() segundos. Obtemos assim uma linha
segundos. Obtemos assim uma linha ![]() paralela ao eixo dos
paralela ao eixo dos
![]() (figura 12).
(figura 12).
Tomemos agora um segundo objecto que está mais alto ![]() metros do que
metros do que ![]() , no instante
, no instante ![]() . Começando em
. Começando em ![]() seguimos
a sua linha de universo durante
seguimos
a sua linha de universo durante ![]() segundos, mas agora
medidos de
acordo com um relógio em
segundos, mas agora
medidos de
acordo com um relógio em ![]() . Obtemos a linha
. Obtemos a linha ![]() . No entanto
como o tempo anda diferentemente às duas altitudes, os dois
pontos
. No entanto
como o tempo anda diferentemente às duas altitudes, os dois
pontos
![]() e
e ![]() não são
simultâneos. Portanto o espaço-tempo é curvo
(figura 12).
não são
simultâneos. Portanto o espaço-tempo é curvo
(figura 12).
Para agravar esta situação, veremos em breve que a própria geometria é ela própria alterada pela presença de um campo gravitacional (veja a discussão sobre o disco rotativo)! Como podemos então definir coordenadas espaciais para acontecimentos no espaço-tempo?
A resposta é Geometria Riemanniana (1826-1866).
Considere a seguinte experiência conceptual: um pulso de luz
é
emitido de um ponto ![]() , numa direcção perpendicular ao movimento
de uma nave, que se move com uma aceleração linear
constante
, numa direcção perpendicular ao movimento
de uma nave, que se move com uma aceleração linear
constante ![]() ,
dirigida para cima, no espaço exterior, longe de qualquer campo
gravitacional (figura 13).
,
dirigida para cima, no espaço exterior, longe de qualquer campo
gravitacional (figura 13).
APPLETT DA VANESSA
APPLETT Cinderella MovAcelerado2.html
No instante em que a luz atinge a outra parede mais afastada, o
elevador subiu uma certa distância. A luz atinge essa parede num
certo ponto ![]() , que está mais abaixo do que o ponto
, que está mais abaixo do que o ponto ![]() . A
diferença de elevação entre
. A
diferença de elevação entre ![]() e
e ![]() é a distância que
o elevador percorreu enquanto a luz estava em trânsito de
é a distância que
o elevador percorreu enquanto a luz estava em trânsito de ![]() para
para ![]() .
.
Um astronauta dentro da nave observa pois que o pulso de luz descreve uma trajectória parabólica (figura 14).
Pelo Princípio de Equivalência, o mesmo será observado pelo astronauta quando a nave não acelera mas está em repouso à superfície da Terra (figura 15).
Ver o teste real da deflexão da luz solar, durante o eclipse de 1919 em Mook (adaptar figura).
Uma plataforma circular (pense na estação espacial do "2001, Odisseia no espaço") roda com velocidade angular constante em torno do seu eixo (figura 31).
Cada ponto da plataforma percorre uma trajectória circular e portanto acelera em direcção ao centro. Um referencial ligado à plataforma é um referencial acelerado no qual a direcção e grandeza da aceleração varia de ponto para ponto. Neste aspecto difere de um referencial uniformemente acelerado no qual todo o ponto tem a mesma aceleração.
Pelo Princípio de Equivalência, este campo de acelerações é equivalente a um campo gravitacional. No entanto, este campo gravitacional não pode ser de tipo Newtoniano - o campo anula-se no centro do disco e cresce proporcionalmente com a distância ao centro, à medida que dele nos afastamos!
Vamos comparar medições de comprimento feitas por um astronauta que habita a plataforma com as que são efectuadas por um observador num referencial de inércia exterior.
Para sermos mais precisos, suponhamos que o observador usa um
referencial de inércia
![]() , e o astronauta um referencial
, e o astronauta um referencial
![]() . O referencial
. O referencial ![]() roda com velocidade
angular uniforme
roda com velocidade
angular uniforme ![]() , relativamente ao referencial de inércia
, relativamente ao referencial de inércia ![]() , de tal forma
que as origens espaciais coincidem sempre, bem como os eixos dos
, de tal forma
que as origens espaciais coincidem sempre, bem como os eixos dos
![]() e
e ![]() (figura 18).
(figura 18).
O astronauta faz experiências no disco (o seu mundo) com relógios e réguas, com o objectivo de chegar a uma definição do significado do tempo e espaço nesse seu mundo.
Para começar ele pega em dois relógios, ![]() e
e ![]() ,
idênticos e coloca
,
idênticos e coloca ![]() no centro do disco e
no centro do disco e ![]() na periferia do
disco. Será que os tic-tacs dos dois relógios são
iguais do
ponto de vista de um observadorfixo no referencial de inércia
na periferia do
disco. Será que os tic-tacs dos dois relógios são
iguais do
ponto de vista de um observadorfixo no referencial de inércia ![]() ?
?
Do ponto de vista deste observador, o relógio no centro tem
velocidade
nula enquanto que o da periferia tem velocidade linear ![]() ,
relativamente a
,
relativamente a ![]() , devido ao movimento de rotação. Portanto,
do ponto de vista de
, devido ao movimento de rotação. Portanto,
do ponto de vista de ![]() , ou do observador
, ou do observador ![]() , o tic-tac do relógio
, o tic-tac do relógio
![]() é mais lento do que o do relógio
é mais lento do que o do relógio ![]() .
.
Portanto não é possível obter uma
definição razoável de
tempo com ajuda de relógios em repouso relativamente ao disco
(referencial ![]() ).
).
Com a medição de comprimentos o mesmo acontece. De
facto, seja
![]() o perímetro do disco e
o perímetro do disco e ![]() o seu
raio, medidos pelo observador
no referencial de inércia
o seu
raio, medidos pelo observador
no referencial de inércia ![]() , usando réguas em repouso relativamente a
esse referencial. Como se sabe, de acordo com a Geometria Euclideana:
, usando réguas em repouso relativamente a
esse referencial. Como se sabe, de acordo com a Geometria Euclideana:
Imaginemos agora réguas de comprimento próprio (de
repouso) ![]() ,
movendo-se solidárias com o disco, em repouso relativamente a
este
(i.e., em repouso relativamente ao referencial
,
movendo-se solidárias com o disco, em repouso relativamente a
este
(i.e., em repouso relativamente ao referencial ![]() ), dispostas
tangencialmente ao longo do seu perímetro, preenchendo-o, e
também ao longo do seu diâmetro. Que valor têm
estes, de
acordo com
), dispostas
tangencialmente ao longo do seu perímetro, preenchendo-o, e
também ao longo do seu diâmetro. Que valor têm
estes, de
acordo com ![]() ?
?
Para imaginar mais precisamente a situação, o
observador ![]() tira uma fotografia instantânea, num certo instante
tira uma fotografia instantânea, num certo instante ![]() . Nesse
instantâneo, cada uma das réguas radiais continua com
comprimento
. Nesse
instantâneo, cada uma das réguas radiais continua com
comprimento ![]() , enquanto que cada uma das tangenciais têm
comprimento
, enquanto que cada uma das tangenciais têm
comprimento ![]() . De facto, como
se sabe da Relatividade Restrita, corpos em movimento sofrem uma
contraçao (de
Lorentz) do seu comprimento na direcção do movimento. No
entanto,
não há qualquer contracção, de acordo com
. De facto, como
se sabe da Relatividade Restrita, corpos em movimento sofrem uma
contraçao (de
Lorentz) do seu comprimento na direcção do movimento. No
entanto,
não há qualquer contracção, de acordo com ![]() , segundo a
direcção do raio do disco (figura 20).
, segundo a
direcção do raio do disco (figura 20).
O perímetro ![]() de um disco circular, do ponto de
vista do astronauta em
de um disco circular, do ponto de
vista do astronauta em ![]() , não
é mais do que o número
, não
é mais do que o número ![]() de réguas
tangenciais que aparecem
no instantâneo, ao longo do perímetro:
de réguas
tangenciais que aparecem
no instantâneo, ao longo do perímetro:
| (19) |
| (20) |
Substituindo ![]() , vem que:
, vem que:
| (21) |
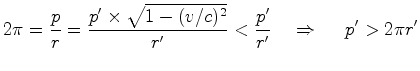
De acordo com o Princípio de Equivalência o referencial
acelerado ![]() do disco é
equivalente a um campo gravitacional. Concluindo:"A Geometria
Euclideana não é válida no disco, nem em geral num
campo gravitacional.
do disco é
equivalente a um campo gravitacional. Concluindo:"A Geometria
Euclideana não é válida no disco, nem em geral num
campo gravitacional.
Tendo reconhecido que gravidade e geometria estão relacionados, Einstein prosseguiu para a hipótese drástica de que o efeito da presença de matéria gravitacional manifesta-se através da distorção do espaço-tempona sua vizinhança. O problema é encontrar a relação entre a distribuição de matéria e a geometria.
Segundo John Wheeler:
Para quem gosta de cálculos mais concretos, eis os detalhes formais da situação anterior:
Comparemos as observações feitas por dois observadores
![]() e
e
![]() , fixos nas origens de dois referenciais
, fixos nas origens de dois referenciais ![]() e
e
![]() . O referencial
. O referencial ![]() roda com velocidade
angular uniforme
roda com velocidade
angular uniforme ![]() , relativamente ao referencial de inércia
, relativamente ao referencial de inércia ![]() , de tal forma
que as origens coincidem sempre bem como os eixos dos
, de tal forma
que as origens coincidem sempre bem como os eixos dos ![]() e
e ![]() (figura 18).
(figura 18). ![]() não é pois um referencial de
inércia. Ignorando as
coordenadas
não é pois um referencial de
inércia. Ignorando as
coordenadas ![]() e
e ![]() , as fórmulas para a mudança
, as fórmulas para a mudança ![]() de
coordenadas são:
de
coordenadas são:
Consideremos agora um ponto ![]() rigidamente ligado
ao referencial
rigidamente ligado
ao referencial
![]() , no com coordenadas
, no com coordenadas ![]() , onde
, onde ![]() é
constante.
é
constante.
Como ![]() está fixo em
está fixo em ![]() , a sua linha de universo é uma
linha recta paralela ao eixo
, a sua linha de universo é uma
linha recta paralela ao eixo ![]() . No entanto, em
. No entanto, em ![]() ,
, ![]() tem
uma velocidade não nula e a sua linha de universo é uma
espiral.
tem
uma velocidade não nula e a sua linha de universo é uma
espiral.
De facto a linha de universo de ![]() , em
, em ![]() , pode ser
parametrizada por:
, pode ser
parametrizada por:
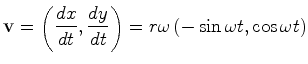 |
(24) |
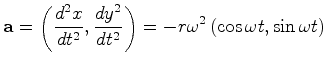 |
(25) |
A limitação de velocidade, imposta pela Relatividade
Restrita, implica que
![]() , donde
, donde ![]() . Portanto o referencial não inercial
. Portanto o referencial não inercial ![]() tem uma fronteira espacial - apenas podemos descrever os acontecimentos
tem uma fronteira espacial - apenas podemos descrever os acontecimentos
![]() que estão dentro do cilindro circular
que estão dentro do cilindro circular
![]() . Como um referencial de inércia não tem
limitações
deste tipo, esta é a primeira diferença que encontramos
para o
referencial não inercial
. Como um referencial de inércia não tem
limitações
deste tipo, esta é a primeira diferença que encontramos
para o
referencial não inercial ![]() .
.
Para medir distâncias recorremos a um reticulado de
réguas no
plano ![]() , dispostas segundo as direcções radiais e circulares
(figura 20).
, dispostas segundo as direcções radiais e circulares
(figura 20).
As réguas que ficam em cima de um círculo são
muito mais
pequenas do que o seu raio, de tal forma a permitir medir o seu
perímetro com uma grande precisão. Meçamos o
perímetro e o
raio do circulo descrito pelo ponto ![]() .
.
Toda a descrição far-se-á relativamente ao
observador ![]() fixo no seu referencial de inércia
fixo no seu referencial de inércia ![]() . Relativamente a este observador, todas as
réguas, alinhadas segundo o perímetro, estão em
movimento, e
portanto contraem-se na direcçao do movimento. No entanto
este movimento circular não tem efeito sobre as réguas
que medem
o raio do círculo. Mais concretamente, as réguas
tangenciais movem-se com
velocidade linear
. Relativamente a este observador, todas as
réguas, alinhadas segundo o perímetro, estão em
movimento, e
portanto contraem-se na direcçao do movimento. No entanto
este movimento circular não tem efeito sobre as réguas
que medem
o raio do círculo. Mais concretamente, as réguas
tangenciais movem-se com
velocidade linear ![]() , e portanto contraem-se por um factor
igual a:
, e portanto contraem-se por um factor
igual a:
Consideremos o círculo de raio ![]() centrado
na origem. Não há
ambiguidade aqui - ambos os observadores concordam àcerca de
distâncias radiais. Do ponto de vista das réguas do
observador
centrado
na origem. Não há
ambiguidade aqui - ambos os observadores concordam àcerca de
distâncias radiais. Do ponto de vista das réguas do
observador
![]() , o círculo tem perímetro
, o círculo tem perímetro ![]() . Mas
. Mas ![]() considera as
réguas tangenciais do referencial
considera as
réguas tangenciais do referencial ![]() mais curtas por um factor
mais curtas por um factor
![]() . Portanto, com estas réguas
. Portanto, com estas réguas
![]() obtem a razão:
obtem a razão:
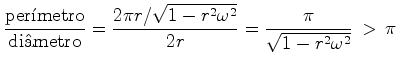 |
(26) |
Vamos agora calcular o tempo próprio do observador ![]() . É claro
que o cálculo deve ser feito num referencial de inércia.
Neste caso, vamos usar
. É claro
que o cálculo deve ser feito num referencial de inércia.
Neste caso, vamos usar
![]() .
.
Como:
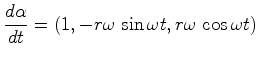
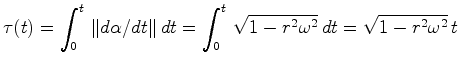 |
(27) |
Em particular, ![]() não é tempo
próprio em
não é tempo
próprio em ![]() , embora seja proporcional ao verdadeiro tempo próprio
, embora seja proporcional ao verdadeiro tempo próprio ![]() . A constante de proporcionalidade
. A constante de proporcionalidade ![]() é sempre inferior a
é sempre inferior a ![]() , e portanto, o relógio de
, e portanto, o relógio de ![]() anda mais devagar do que o de
anda mais devagar do que o de ![]() . Sabemos já que relógios que se movem andam mais
devagar. Como a velocidade cresce com
. Sabemos já que relógios que se movem andam mais
devagar. Como a velocidade cresce com ![]() , o mesmo acontece com a dilatação do tempo (figura 22).
, o mesmo acontece com a dilatação do tempo (figura 22).
Variando a aceleração de um observador num espaço-tempo plano, podemos, de acordo com o Princípio de Equivalência, imitar um qualquer campo gravitacional. Então porque necessitamos de espaços-tempo curvos ?
Quando discutimos o Princípio de Equivalência, suposemos que o campo gravitacional era uniforme, isto é, que relativamente a um observador de inércia, a aceleração de todos os corpos que caiem é sempre a mesma (em direcção e grandeza). No entanto isto não corresponde à realidade - é só uma aproximação. De facto, a aceleração devida à gravidade varia de ponto para ponto.
Consideremos as seguintes situações não locais:
 |
 |
 |
 |
Agora, o observador pode distinguir o campo uniforme da situação S1. do campo gravitacional terrestre não uniforme da situação S3.. Novamente, em queda livre, os corpos viajam em geodésicas que convergem (ou divergem) como na situação S4.
FIGURAS
Estes novos efeitos, chamados "efeitos maré" (tidal effects) da gravidade são provocados pela não uniformidade do campo gravitacional, que varia de ponto para ponto.
São, de facto, muito ténues quando analisados localmente. Por outras palavras, uma cápsula muito pequena em queda livre, num intervalo de tempo muito curto, é, em primeira aproximação, um referencial de inércia. Este referencial diz-se por isso um referencial local de inércia.
Na presença de um campo gravitacional, por exemplo, na presença de uma massa grande (Terra, Sol, ...), duas partículas teste que se movem com a mesma velocidade inicial ao longo de duas trajectórias espaciais próximas, em geral não continuam paralelas, mas aceleram gradualmente uma relativamente à outra, devido à não uniformidade do campo gravitacional.
Esta aceleração relativa de partículas em queda
livre é completamente análoga à
situação seguinte. Imaginemos dois viajantes que partem
de dois pontos próximos ![]() e
e ![]() no equador da esfera, ambos em direcção ao
pólo norte, ao longo de dois meridianos (figura 27).
no equador da esfera, ambos em direcção ao
pólo norte, ao longo de dois meridianos (figura 27).
As trajectórias dos dois viajantes são inicialmente paralelas, mas aproximam-se gradualmente uma da outra até se encontrarem no pólo norte.
Seja ![]() a parametrizaçãode um dos meridianos, por comprimento de
arco, com
a parametrizaçãode um dos meridianos, por comprimento de
arco, com ![]() , e seja
, e seja ![]() a distância entre
a distância entre ![]() e o outro meridiano, medida ao longo do
paralelo que passa em
e o outro meridiano, medida ao longo do
paralelo que passa em
![]() . Então:
. Então:
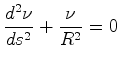 |
(28) |
Como ![]() é a curvatura de Gauss da esfera,
podemos escrever:
é a curvatura de Gauss da esfera,
podemos escrever:
Numa superfície de curvatura negativa, por exemplo, geodésicas inicialmente paralelas afastam-se uma da outra (figura 28).
A analogia entre as duas situações referidas:
Partindo do seu Princípio de Equivalência, Einstein concluiu que gravidade não é uma força, como Newton julgava, mas sim curvatura do espaço-tempo. A fonte desta curvatura é matéria - um corpo material cria um campo gravitacional que deforma ou "curva" o espaço-tempo envolvente.
Generalizando a lei de inércia de Newton, que diz que partículas livres deslocam-se segundo geodésicas (linhas rectas) no espaço-tempo plano da Relatividade Restrita (gravidade zero = curvatura nula), Einstein afirma que partículas livres devem seguir geodésicas no espaço-tempo com curvatura. Portanto, todos os objectos materais, desde uma maçã até um planeta, movem-se ao longo de geodésicas do espaço-tempo, a menos que sejam impedidas por qualquer força exterior. O mesmo acontece com os raios de luz.
Consideremos o movimento de um planeta (a Terra, por exemplo) em volta do Sol. Duas explicações em confronto:
FIGURA
Vemos pois que, ao considerar o movimento dos corpos no espaço, e ao usar o tempo como uma entidade absoluta e independente, Newton teve que introduzir uma força para explicar o comportamento de uma massa teste junto de uma outra. Einstein não precisa de introduzir uma força para explicar isso. A explicação é puramente geométrica
Façamos o transporte paralelo de um vector tangente ao longo de
um (pequeno) triângulo geodésico ![]() , de tal forma que o
vector, durante o seu movimento, faz sempre um ângulo constante
com cada um dos três lados desse triângulo.
, de tal forma que o
vector, durante o seu movimento, faz sempre um ângulo constante
com cada um dos três lados desse triângulo.
O movimento faz-se no sentido positivo (anti-horário).
A Holonomia ![]() do
triângulo geodésico
do
triângulo geodésico ![]() define-se como sendo o menor ângulo
orientado formado pela posição inicial do vector com a
sua
posição final, depois de completado um percurso completo
ao longo
do perímetro de
define-se como sendo o menor ângulo
orientado formado pela posição inicial do vector com a
sua
posição final, depois de completado um percurso completo
ao longo
do perímetro de ![]() .
.
É possível mostrar que (Gauss-Bonnet):
Portanto:
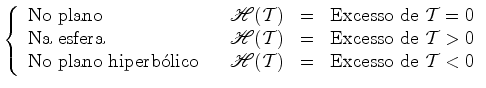
A curvatura de Gauss ![]() , em cada um destes modelos (de curvatura
constante) pode ser definida por:
, em cada um destes modelos (de curvatura
constante) pode ser definida por:
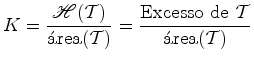

| Plano | Esfera | Curvatura negativa |
| Rectas perpendiculares | Geodésicas perpendiculares | Geodésicas perpendiculares |
| a uma mesma recta | a uma mesma linha | a uma mesma linha |
| são paralelas | convergem | divergem |
| Soma dos ângulos | Soma dos ângulos | Soma dos ângulos |
| de um triângulo (geodésico) | de um triângulo (geodésico) | de um triângulo (geodésico) |
| é igual a |
é superior a |
é inferior a |
| Perímetro de um círculo | Perímetro de um círculo | Perímetro de um círculo |
| de raio |
de raio |
de raio |
| é igual a |
é inferior a |
é superior a |
| Curvatura nula | Curvatura positiva (constante) | Curvatura negativa (constante) |
| |
|
|
| Plano |
Esfera |
Plano hiperbólico |
| Rectas perpendiculares a uma mesma recta são paralelas |
Geodésicas perpendiculares a uma mesma linha convergem |
Geodésicas perpendiculares a uma mesma linha divergem |
| A soma dos ângulos internos de um triângulo geodésico é igual a |
A soma dos ângulos internos de um triângulo geodésico é superior a |
A soma dos ângulos internos de um triângulo geodésico é inferior a |
| O perímetro de um
círculo de raio é igual a |
O perímetro de um
círculo de raio é inferior a |
O perímetro de um
círculo de raio é superior a |
| Curvatura K=0 |
Curvatura K=+1 | Curvatura K=-1 |
Do princípio da covariância geral, Einstein argumenta que todas as leis da Física devem ser expressas como equações tensoriais para que elas se transformem convenientemente sob mudanças de coordenadas.
Consideremos então um referencial em queda livre num campo gravitacional. Um tal referencial é um referencial de inércia, e portanto um objecto caindo com ele move-se linearmente e portanto ao longo de uma geodésica nesse referencial. Como as geodésicas são definidas por equações tensoriais, o princípio da covariância geral garante que todos os observadores dirão que todos os objectos em queda livre seguem trajectórias que são geodésicas (temporais) do espaço-tempo. Poratnto as equações do movimento num campo gravitacional são equações das geodésicas.
Por outro lado, a métrica num sistema de coordenadas qualquer define o campo gravitacional nessas coordenadas. Devido à relacção entre campo e métrica, as equaçõesdo campo dizem-nos não apenas como as fontes de gravitação determinam o campo mas também como elas determinam a curvatura do espaço-tempo. A conclusão revolucionária de Einstein é pois:
Pôr aqui a noção moderna de covariância (diff-invariância) e o "hole argument" (Rovelli, Norton,etc...)