O disco rotativo
 |
|||||||||||
|
Uma plataforma circular (pense na estação
espacial do
"2001,
Odisseia no espaço") roda com velocidade angular constante em
torno do seu eixo:
Cada ponto da plataforma percorre uma trajectória circular e portanto acelera em direcção ao centro. Um referencial ligado à plataforma é um referencial acelerado no qual a direcção e grandeza da aceleração varia de ponto para ponto. Neste aspecto difere de um referencial uniformemente acelerado no qual todo o ponto tem a mesma aceleração. Pelo Princípio de Equivalência, este campo de acelerações é equivalente a um campo gravitacional. No entanto, este campo gravitacional não pode ser de tipo Newtoniano - o campo anula-se no centro do disco e cresce proporcionalmente com a distância ao centro, à medida que dele nos afastamos! Vamos comparar
medições de tempo e comprimento feitas por:
Para
sermos mais precisos,
suponhamos que:
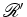 roda com
velocidade
angular uniforme roda com
velocidade
angular uniforme 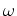 , relativamente ao referencial de inércia
, relativamente ao referencial de inércia 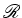 , de tal forma
que as origens espaciais coincidem sempre, bem como os eixos dos
, de tal forma
que as origens espaciais coincidem sempre, bem como os eixos dos 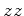 e e 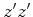 : :
O astronauta faz experiências no disco (o seu mundo) com relógios e réguas, com o objectivo de chegar a uma definição do significado do tempo e espaço nesse seu mundo. |
|||||||||||
| Medição dos tempos |
|||||||||||
|
Para
começar ele pega em
dois relógios, Do
ponto de vista deste
observador, o relógio no centro tem
velocidade
nula enquanto que o da periferia tem velocidade linear
Portanto não
é possível obter uma
definição razoável de
tempo com ajuda de relógios em repouso relativamente ao disco
(referencial |
|||||||||||
| Medição de comprimentos | |||||||||||
|
Com
a medição de
comprimentos o mesmo acontece. De
facto, seja
Imaginemos
agora
réguas de comprimento próprio
(de
repouso)
Para
imaginar mais precisamente a
situação, o
observador
De facto, como
se sabe da Relatividade Restrita, corpos em movimento sofrem uma
contracção (de
Lorentz) do seu comprimento na direcção do movimento. No
entanto,
não há qualquer contracção, de acordo com

O perímetro
Por outro lado, o observador 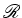 , ao examinar o instantâneo, vê
o mesmo número
, ao examinar o instantâneo, vê
o mesmo número 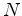 de
réguas ao longo da
periferia do disco, mas
agora, cada uma com um comprimento de
réguas ao longo da
periferia do disco, mas
agora, cada uma com um comprimento 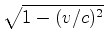 . Portanto, de
acordo com
. Portanto, de
acordo com 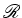 , o perímetro do disco é:
, o perímetro do disco é:
Substituindo
Mas como, por outro lado, 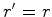 , e
, e 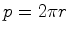 , vem que:
, vem que:
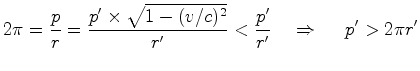
|
|||||||||||
De
acordo com o Princípio
de Equivalência o referencial
acelerado 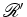 do disco
é
equivalente a um campo gravitacional. Concluindo: do disco
é
equivalente a um campo gravitacional. Concluindo:
|
|||||||||||
|
Tendo reconhecido que gravidade e geometria estão relacionados, Einstein prosseguiu para a hipótese drástica de que o efeito da presença de matéria gravitacional manifesta-se através da distorção do espaço-tempo na sua vizinhança. O problema é encontrar a relação entre a distribuição de matéria e a geometria. Segundo John Wheeler:
 |
|||||||||||
| Cálculos: |
|||||||||||
|
|||||||||||
|
|
|||||||||||
| Próximo: Curvatura Anterior: Consequências do Princípio de Equivalência Regresso ao Índice |
|||||||||||

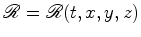 ,
e o
,
e o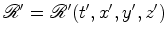
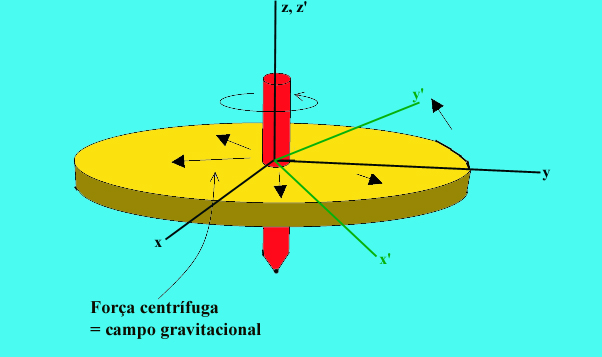
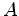 e
e 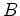 ,
idênticos, e coloca
,
idênticos, e coloca 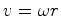 ,
relativamente a
,
relativamente a 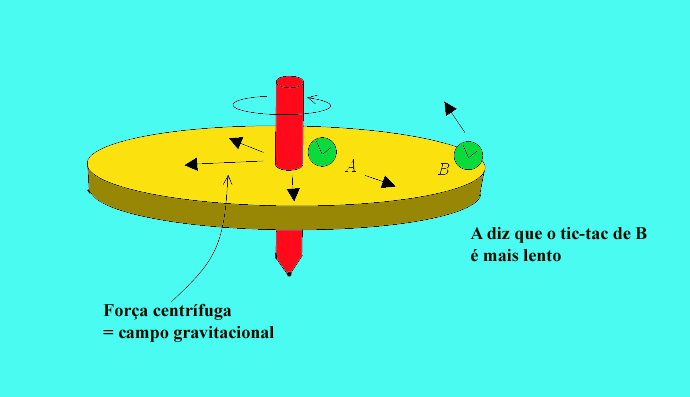
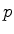 o perímetro do disco e
o perímetro do disco e 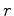 o seu
raio, medidos pelo observador
no referencial de inércia
o seu
raio, medidos pelo observador
no referencial de inércia 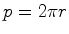
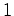 ,
movendo-se solidárias com o disco, em repouso relativamente a
este
(i.e., em repouso relativamente ao referencial
,
movendo-se solidárias com o disco, em repouso relativamente a
este
(i.e., em repouso relativamente ao referencial 
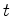 . Nesse
instantâneo, cada uma das réguas radiais continua com
comprimento
. Nesse
instantâneo, cada uma das réguas radiais continua com
comprimento 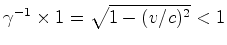
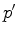 de um disco circular, do ponto de
vista do astronauta em
de um disco circular, do ponto de
vista do astronauta em 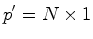
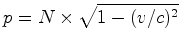
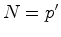 , vem que:
, vem que: 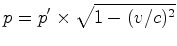
 e
e  , fixos nas
origens de dois referenciais
, fixos nas
origens de dois referenciais 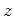 e
e 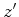 , as fórmulas para a mudança
, as fórmulas para a mudança 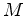 de
coordenadas são:
de
coordenadas são: 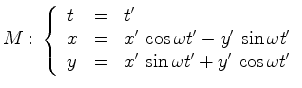
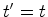 , uma vez que
, uma vez que 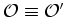 durante todo o
movimento.
durante todo o
movimento. 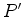 rigidamente ligado
ao referencial
rigidamente ligado
ao referencial 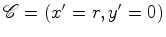 , onde
, onde 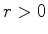 é
constante.
é
constante. 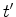 . No entanto, em
. No entanto, em 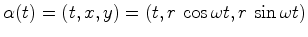
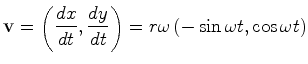
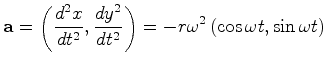
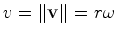 é pois directamente
proporcional ao raio
é pois directamente
proporcional ao raio 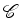 ) tem grandeza
) tem grandeza 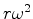 e aponta para dentro (aceleração centrípeta).
e aponta para dentro (aceleração centrípeta).
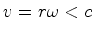 ,
donde
,
donde 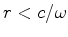 . Portanto o referencial não inercial
. Portanto o referencial não inercial 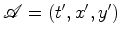 que
estão dentro do cilindro circular
que
estão dentro do cilindro circular 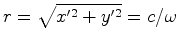 .
Como um referencial de inércia não tem
limitações
deste tipo, esta é a primeira diferença que encontramos
para o
referencial não inercial
.
Como um referencial de inércia não tem
limitações
deste tipo, esta é a primeira diferença que encontramos
para o
referencial não inercial 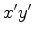 , dispostas segundo as direcções radiais e circulares
(figura 20).
, dispostas segundo as direcções radiais e circulares
(figura 20). 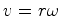 , e portanto contraem-se por um factor
igual a:
, e portanto contraem-se por um factor
igual a: 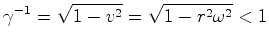
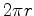 . Mas
. Mas 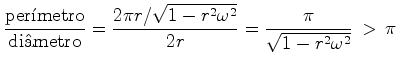
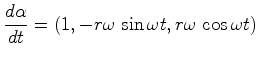
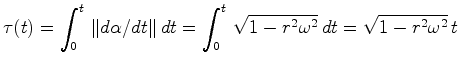
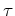 . A constante de proporcionalidade
. A constante de proporcionalidade 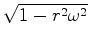 é sempre inferior a
é sempre inferior a