Dilatação do tempo |
||||||||||||||||||
 |
||||||||||||||||||
|
Considere mais uma vez um
autocarro que se move com velocidade
constante
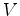 relativamente à paragem.
Seja relativamente à paragem.
Seja  um referencial
ligado à paragem e um referencial
ligado à paragem e  um referencial ligado ao autocarro. um referencial ligado ao autocarro. Na
parede lateral do autocarro está um passageiro
No referencial onde 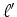 é a largura do autocarro, medida em é a largura do autocarro, medida em  . .
Note
que os acontecimentos
Seja
Note
que agora os acontecimentos Durante
o intervalo onde 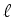 é a largura do
autocarro, medida em é a largura do
autocarro, medida em  .
.
Como a velocidade da luz é igual a Resolvendo em ordem a 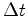 estas duas últimas igualdades, (20)
e (21), obtemos:
estas duas últimas igualdades, (20)
e (21), obtemos:onde o factor de Lorentz 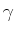 é dado por: é dado por:
Como
o autocarro se move unicamente segundo a direcção do eixo
dos x's, é natural supôr que
Como já vimos, no
referencial
 , ligado ao autocarro, o raio
regressa ao mesmo ponto de partida (o que não acontece, de
acordo
com o referencial
, ligado ao autocarro, o raio
regressa ao mesmo ponto de partida (o que não acontece, de
acordo
com o referencial  , como está bem claro nos applets anteriores).
, como está bem claro nos applets anteriores).O
intervalo de tempo entre dois acontecimentos que ocorrem no mesmo
local (espacial) diz-se o tempo próprio entre esses dois
acontecimentos. O tempo próprio é o menor tempo
medido -
pode ser medido por um mesmo relógio situado no local onde
ocorrem
os acontecimentos. Qualquer outro tempo (impróprio)
representa a
diferença de leituras de dois relógios distintos. |
||||||||||||||||||
| Concluindo: |
|
|||||||||||||||||
|
O tic-tac de um relógio em movimento uniforme
é mais lento
quando observado por um referencial estacionário:
Esta "dilatação do tempo" ocorre qualquer
que seja o tipo de "relógio". Se assim não fosse, o
princípio da relatividade seria violado - se existisse um
relógio insensível à dilatação
temporal, poderíamos usá-lo para distinguir certos
referenciais de inércia. |
||||||||||||||||||
| Decaímento de muões |
O decaímento de muões a alta velocidade (relativamente à terra) suporta experimentalmente esta predição da teoria. De
facto a duração de vida própria de um muão
é
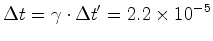
A distância que o
muão percorre, no referencial ligado à terra, é
pois de cerca de |
|||||||||||||||||
| Página seguinte: Contracção do
comprimento Página anterior: Relatividade da noção de simultaneidade Índice |
 que, no instante
que, no instante 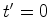 , dispara um flash emitindo um raio luminoso (acontecimento
, dispara um flash emitindo um raio luminoso (acontecimento 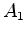 ), que segue na direcção da parede oposta, aí
é reflectido (acontecimento
), que segue na direcção da parede oposta, aí
é reflectido (acontecimento 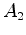 ), e regressa ao ponto de partida (acontecimento
), e regressa ao ponto de partida (acontecimento 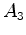 ):
): 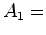
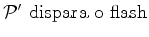

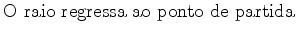
 Analisemos
a experiência no referencial
Analisemos
a experiência no referencial
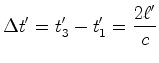
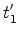 e
e 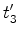 são
medidos por um mesmo relógio (o do passageiro
são
medidos por um mesmo relógio (o do passageiro 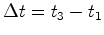 o
intervalo de tempo entre o instante
o
intervalo de tempo entre o instante 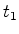 em que o raio
parte (o flash dispara) e o instante
em que o raio
parte (o flash dispara) e o instante 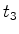 em
que regressa, medido por testemunhas
em
que regressa, medido por testemunhas 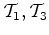 (observadores)
ligados a
(observadores)
ligados a 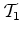 e
e 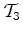 ).
). 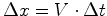 . De acordo com
esses obervadores, o raio percorre uma trajectória cujo
comprimento total é:
. De acordo com
esses obervadores, o raio percorre uma trajectória cujo
comprimento total é: 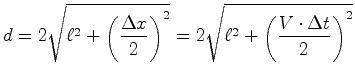
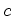 , em ambos os referenciais, tem-se
também que:
, em ambos os referenciais, tem-se
também que: 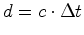
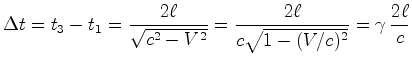
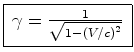
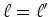 (de facto, não há
deformação de comprimento segundo direcções
perpendiculares ao movimento). Sendo assim, é possível
relacionar os dois intervalos de tempo
(de facto, não há
deformação de comprimento segundo direcções
perpendiculares ao movimento). Sendo assim, é possível
relacionar os dois intervalos de tempo 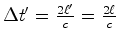 e
e 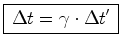
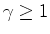 .
.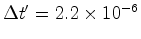 segundos. O
muão desloca-se relativamente
à terra com uma velocidade uniforme de
segundos. O
muão desloca-se relativamente
à terra com uma velocidade uniforme de 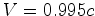 . Logo o factor
de Lorentz é
. Logo o factor
de Lorentz é 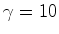 e o tempo de percurso
(médio) de um
muão, antes da sua desintegração, é:
e o tempo de percurso
(médio) de um
muão, antes da sua desintegração, é: 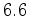 Km, suficiente para explicar a existência
de muões detectados ao nível do mar !!
Km, suficiente para explicar a existência
de muões detectados ao nível do mar !!