A numerical semigroup ![]() is a subset of
is a subset of
![]() that is closed under
addition,
that is closed under
addition, ![]() and generates
and generates
![]() as a group (
as a group (
![]() and
and
![]() denote the
set of integers and nonnegative integers, respectively). It is well known (see
for instance [2,8,13]) that if
denote the
set of integers and nonnegative integers, respectively). It is well known (see
for instance [2,8,13]) that if ![]() is a numerical semigroup,
then the set
is a numerical semigroup,
then the set
![]() has finitely many elements. The greatest integer
not belonging to
has finitely many elements. The greatest integer
not belonging to ![]() is called the Frobenius number of
is called the Frobenius number of ![]() , usually
denoted by
, usually
denoted by
![]() . Moreover,
. Moreover, ![]() admits a unique minimal system of generators
admits a unique minimal system of generators
![]() (that is,
(that is,
![]() and no proper subset of
and no proper subset of
![]() generates
generates ![]() ). The
integers
). The
integers ![]() and
and ![]() are known as the multiplicity and
embedding dimension of
are known as the multiplicity and
embedding dimension of ![]() , and they are denoted by
, and they are denoted by
![]() and
and ![]() , respectively. For a given
, respectively. For a given
![]() , we will denote by
, we will denote by
![]() the submonoid of
the submonoid of
![]() generated by
generated by ![]() . The monoid
. The monoid
![]() is a numerical semigroup if and only if
is a numerical semigroup if and only if ![]() (
(![]() stands
for greatest common divisor).
There is a large amount of literature concerning the study of one-dimensional
analitically unramified domains via their valuation semigroups (see for
instance [3,5,6,7,10,15,16]).
One of the properties studied for this kind of rings using this approach has
been the Arf property. From [1], Lipman in [11] introduces
and motivates the study of Arf rings; the characterization given in that paper
of Arf rings in terms of its semigroup of values gives rise to the notion of
Arf semigroup (see also [2] for the connection between the Arf
property of a one-dimensional analitically irreducible domain and the Arf
property of its semigroup of values). In [14,4] it is
studied the relationship between the Pythagorean property of a real curve germ
and the Arf property of its value numerical semigroup.
A numerical semigroup
stands
for greatest common divisor).
There is a large amount of literature concerning the study of one-dimensional
analitically unramified domains via their valuation semigroups (see for
instance [3,5,6,7,10,15,16]).
One of the properties studied for this kind of rings using this approach has
been the Arf property. From [1], Lipman in [11] introduces
and motivates the study of Arf rings; the characterization given in that paper
of Arf rings in terms of its semigroup of values gives rise to the notion of
Arf semigroup (see also [2] for the connection between the Arf
property of a one-dimensional analitically irreducible domain and the Arf
property of its semigroup of values). In [14,4] it is
studied the relationship between the Pythagorean property of a real curve germ
and the Arf property of its value numerical semigroup.
A numerical semigroup ![]() is an Arf numerical semigroup if for every
is an Arf numerical semigroup if for every
![]() such that
such that
![]() , we have that
, we have that
![]() (see
[2, Theorem I.3.4] for fifteen alternative characterizations of
this property).
We deduce that the intersection of two Arf numerical semigroups is
again an Arf numerical semigroup. This allows us to define the Arf numerical semigroup generated by
(see
[2, Theorem I.3.4] for fifteen alternative characterizations of
this property).
We deduce that the intersection of two Arf numerical semigroups is
again an Arf numerical semigroup. This allows us to define the Arf numerical semigroup generated by ![]() (
(![]() ) as the intersection of all Arf numerical semigroups containing
) as the intersection of all Arf numerical semigroups containing
![]() (and thus
(and thus
![]() ), and will denote it by
), and will denote it by
![]() . If
. If
![]() , we say that
, we say that ![]() is an Arf system
of generators of
is an Arf system
of generators of ![]() , and we will say that
, and we will say that ![]() is minimal if no
proper subset of
is minimal if no
proper subset of ![]() is an Arf system of generators of
is an Arf system of generators of ![]() . For a numerical
semigroup
. For a numerical
semigroup ![]() ,
,
![]() will be also called the Arf closure of
will be also called the Arf closure of ![]() .
Observe that if we are given
.
Observe that if we are given
![]() with
with ![]() , then
, then
![]() must contain the set of all the elements
of the form
must contain the set of all the elements
of the form ![]() with
with
![]() and
and
![]() . It
must also contain the set of elements that are derived from those obtained
above using the same rule and so on. This motivates the following results.
We define a submonoid of
. It
must also contain the set of elements that are derived from those obtained
above using the same rule and so on. This motivates the following results.
We define a submonoid of
![]()
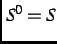 ,
,
-
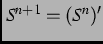 .
.
As we pointed out before, every numerical semigroup admits a unique minimal system of generators, and we prove that every Arf numerical semigroup has a unique minimal system of generators. A binary tree is a rooted tree such that every vertex has at most two sons (see [9]). Now, we describe a recursive procedure that arranges the set of all Arf numerical semigroups in a binary tree whose root is
Let
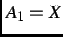 ,
,
-
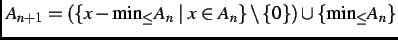 .
.
-
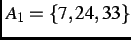 ,
,
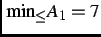 ,
,
-
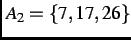 ,
,
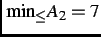 ,
,
-
 ,
,
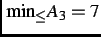 ,
,
-
 ,
,
 ,
,
-
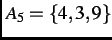 ,
,
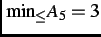 ,
,
-
 ,
,
Next: Bibliography

Sponsored in part by the FCT approved projects POCTI 32817/99 and POCTI/MAT/37670/2001 in participation with the European Community Fund FEDER and by FCT through Centro de Matemática da Universidade do Porto. Also sponsored in part by FCT, the Faculdade de Ciências da Universidade do Porto, Programa Operacional Ciência, Tecnologia, Inovação do Quadro Comunitário de Apoio III, and by Caixa Geral de Depósitos.
![\begin{figure}
\xymatrix @R=1pc @C=1pc{
& & & {\begin{matrix}{\mathbb{N}}={\r...
...trix}{\rm Arf}(2,9),\\ g=7\end{matrix}}\ar@{..}[d] \\
& & & & }
\end{figure}](img36.png)