|
O compasso perfeito é composto por quatro partes
articuladas,
representadas na figura seguinte:
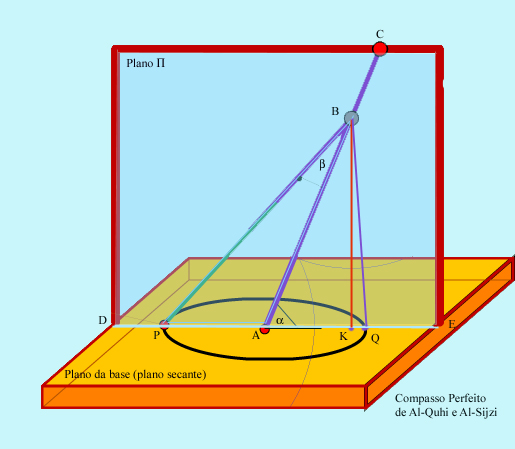
e que passamos a descrever:
- 1.
- o ``plano da base" que contem a "recta do centro"
 . . - 2.
- o ``eixo do compasso"
 , que pode
rodar em torno do ``centro" , que pode
rodar em torno do ``centro"  ,
mantendo-se sempre no plano vertical ,
mantendo-se sempre no plano vertical  , que
é perpendicular ao plano da base, intersectando-o segundo a
recta , que
é perpendicular ao plano da base, intersectando-o segundo a
recta  . . - 3.
- a ``recta do vértice"
 , que pode
rodar em torno do ponto , que pode
rodar em torno do ponto  ,
chamado o ``vértice". Consideramos a
posiçãoinicial desta recta ,
chamado o ``vértice". Consideramos a
posiçãoinicial desta recta  , no plano , no plano  , quando
fazemos a escolha do ângulo no vértice , quando
fazemos a escolha do ângulo no vértice
 . .
De seguida fazemos esta recta rodar em torno do eixo 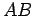 , gerando
desta forma um cone de revolução , gerando
desta forma um cone de revolução
 de vértice
de vértice 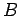 (supondo
que (supondo
que  . Neste caso
obtem-se um plano, é
claro!). . Neste caso
obtem-se um plano, é
claro!).
- 4.
- A recta
 é ela própria o suporte de um tira-linhas, que pode
deslizar nesta recta, para que a sua extremidade
é ela própria o suporte de um tira-linhas, que pode
deslizar nesta recta, para que a sua extremidade  trace uma
curva (de facto, uma cónica) no plano da base. trace uma
curva (de facto, uma cónica) no plano da base.
O applet seguinte ilustra esta
descrição, bem como os papeis desempenhados pelos
vários elementos do compasso perfeito.
|
|
|
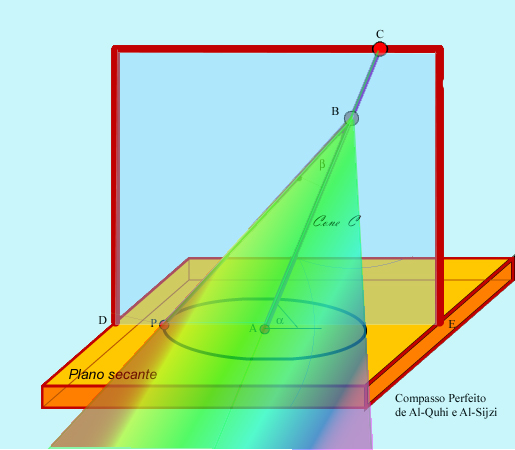
Tudo depende do ângulo
 e do
ângulo e do
ângulo  ,
formado pelo eixo do
compasso com o plano da base (ver a figura anterior). ,
formado pelo eixo do
compasso com o plano da base (ver a figura anterior).
Seja  a perpendicular baixada de a perpendicular baixada de 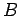 sobre o
plano da base. A natureza da
curva, traçada por sobre o
plano da base. A natureza da
curva, traçada por  , depende do ângulo , depende do ângulo
 . .
Temos que:
Designemos por  o cone de revolução de
vértice o cone de revolução de
vértice 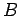 ,
gerado ao rodar a recta do vértice ,
gerado ao rodar a recta do vértice  , em torno do eixo , em torno do eixo 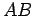 . .
Portanto:
a curva traçada por  é uma elipse. é uma elipse.
De facto, neste caso, o plano da base (plano secante)
intersectará todas as geratrizes do cone
 numa mesma folha,
e por isso, a curva que não é mais do que a
intersecção do
cone numa mesma folha,
e por isso, a curva que não é mais do que a
intersecção do
cone  com este plano secante, é uma
elipse. com este plano secante, é uma
elipse.
|
|
|
 ,
 é uma parábola. é uma parábola.
De facto, neste caso, o plano da base (plano secante)
será paralelo à geratriz  , como se representa na figura
seguinte. , como se representa na figura
seguinte.
|
|


 é uma elipse.
é uma elipse.
 ,
,  é uma parábola.
é uma parábola.

 é um ramo de hipérbole.
é um ramo de hipérbole.

 .
.  , que pode
rodar em torno do ``centro"
, que pode
rodar em torno do ``centro"  ,
mantendo-se sempre no plano vertical
,
mantendo-se sempre no plano vertical  , que
é perpendicular ao plano da base, intersectando-o segundo a
recta
, que
é perpendicular ao plano da base, intersectando-o segundo a
recta  , que pode
rodar em torno do ponto
, que pode
rodar em torno do ponto 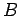 ,
chamado o ``vértice". Consideramos a
posiçãoinicial desta recta
,
chamado o ``vértice". Consideramos a
posiçãoinicial desta recta  .
.
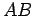 , gerando
desta forma um cone de revolução
, gerando
desta forma um cone de revolução
 de vértice
de vértice  . Neste caso
obtem-se um plano, é
claro!).
. Neste caso
obtem-se um plano, é
claro!).  ,
formado pelo eixo do
compasso com o plano da base (ver a figura anterior).
,
formado pelo eixo do
compasso com o plano da base (ver a figura anterior).  a perpendicular baixada de
a perpendicular baixada de  .
.  , em torno do eixo
, em torno do eixo 
 , como se representa na figura
seguinte.
, como se representa na figura
seguinte.