


2nd Porto Meeting on
MATHEMATICS for INDUSTRY
MATHEMATICS for INDUSTRY
16th to 18th
April 2010
| home |
| about the meeting |
| main speakers/courses |
| talks/posters |
| registration form |
| study group |
| organizers |
| travel & accomodations |
| participants |
| poster |
| timetable |
| contacts |
| documentation |
| impact |
Main Speakers and courses
- Luigi Barletti (Dipartimento di Matematica "Ulisse Dini", Universita' di Firenze, Italia)
Mathematical
modeling of quantum electronic devices
Abstract: The miniaturization reached by semiconductor technology has brought electronic devices on the border of (and in many cases inside) the quantum realm.
Applied mathematics has, therefore, the difficult task of providing electronic industry with easy-to-handle models of systems in which the macroscopic behavior of the device is determined by the microscopic, and often non-intuitive, quantum dynamics.
This short course is aimed to present the basic mathematical tools (Wigner functions, Chapman-Enskog expansion, Entropy principle) that allow to derive fluid-dynamical-like models starting from "first principles" , represented by quantum kinetic equations.
Examples of applications to innovative devices exploiting quantum effects, such as interband tunneling or spin-orbit interactions, will be briefly discussed.
Abstract: The miniaturization reached by semiconductor technology has brought electronic devices on the border of (and in many cases inside) the quantum realm.
Applied mathematics has, therefore, the difficult task of providing electronic industry with easy-to-handle models of systems in which the macroscopic behavior of the device is determined by the microscopic, and often non-intuitive, quantum dynamics.
This short course is aimed to present the basic mathematical tools (Wigner functions, Chapman-Enskog expansion, Entropy principle) that allow to derive fluid-dynamical-like models starting from "first principles" , represented by quantum kinetic equations.
Examples of applications to innovative devices exploiting quantum effects, such as interband tunneling or spin-orbit interactions, will be briefly discussed.
- Jorge Orestes Cerdeira (Instituto Superior de Agronomia, Universidade Tecnica de Lisboa)
Applications of
discrete mathematics in
industry
Abstract: Industry is a prolific field of applications for different research areas in mathematical sciences. We will focus on applications of discrete mathematics in industry. Topics such as covering, assignment, scheduling and routing will be exploited and identified as adequate models
for some problems faced by industry.
Abstract: Industry is a prolific field of applications for different research areas in mathematical sciences. We will focus on applications of discrete mathematics in industry. Topics such as covering, assignment, scheduling and routing will be exploited and identified as adequate models
for some problems faced by industry.
- Robert Mattheij (Dept of Mathematics and Computer Science, Eindhoven, The Netherlands)
Industrial problems
involving morphology and flow
Abstract: Three lectures by Bob Mattheij
Abstract: Three lectures by Bob Mattheij
1. Blowing
of glass forms
The morphology of viscous bodies can be
described by Stokes’equation. An essential part in such problems is the
kind of boundary condition. In particular for moving boundaries we
encounter numerical difficulties. We will focus on the modelling and
simulation of a (glass) container and describe a way to deal with the
latter boundary. In reality one often has to produce a certain
prescribed shape of the container. The resulting inverse problem
provides for some additional difficulties. We will discus how to deal
with the latter as well.2. Cooling
of blades in turbines
Turbines (jet engines or gasturbines) have
rotors at the hot end that need to be cooled. This cooling is done by
blowing cool air through the blade (internal cooling) or through holes
in the surface (to provide for film cooling). A variety of methods is
used to drill these holes (electrochemistry or laser drilling),
Simulation of the flow eventually provides for a complex problem that
is tackled by a domain decomposition technique.3.
Conservation of mass in
evolution problems
A typical concern in numerical modelling
of problems is how to conserve mass. We will discuss a typical
evolutionary problem arising from practice that gives rise to
undesirably large errors in the mass, unless special precautions are
taken. If we assume some form of symmetry in the body under
consideration we can reformulate the problem in such a way that a
symplectic method can be used, leading to numerical mass conservation.- Jon Selig (Faculty of Business, Computing and Information Management London South Bank University)
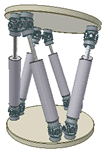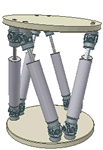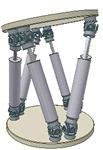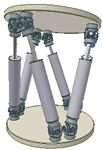
Robotics
and Geometry
Abstract: The group of rigid-body displacements plays a fundamental role in robotics and computer vision. These lectures will introduce this Lie group and its Lie algebra. This will be done by looking at the problem of Robot Kinematics for both serial and parallel manipulators. The group of rigid-body displacements can be viewed as an open set in a six-dimensional quadric called the Study quadric. The geometry of this space will be explored and used to describe some questions concerning rigid-body motions.
Abstract: The group of rigid-body displacements plays a fundamental role in robotics and computer vision. These lectures will introduce this Lie group and its Lie algebra. This will be done by looking at the problem of Robot Kinematics for both serial and parallel manipulators. The group of rigid-body displacements can be viewed as an open set in a six-dimensional quadric called the Study quadric. The geometry of this space will be explored and used to describe some questions concerning rigid-body motions.