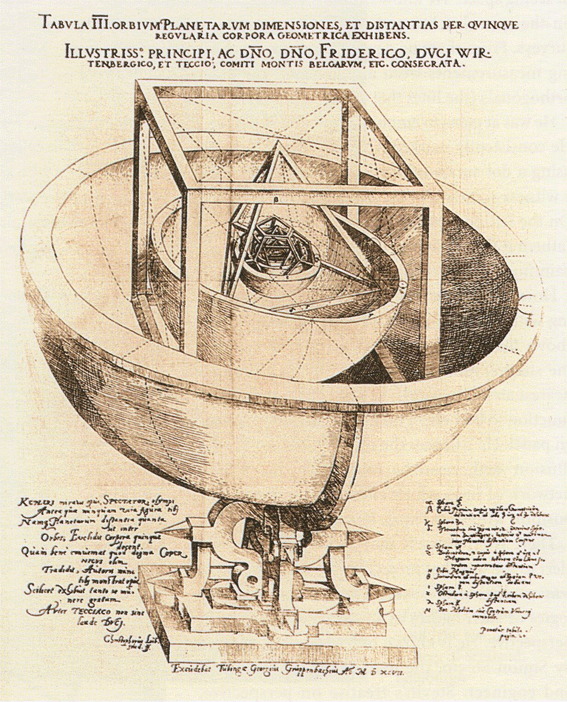
A teoria planetária de Kepler




   A teoria de Kepler sobre o papel desempenhado pelos sólidos regulares no universo, é um pouco mais "científica" do que a teoria atómica de Platão. Na altura, eram seis os planetas conhecidos: Mercúrio, Vénus, Terra, Marte, Júpiter e Saturno.

   Kepler, influenciado pela teoria de Copérnico, segundo a qual os planetas se movimentam à volta do Sol, procurou encontrar relações numéricas para explicar a existência de exactamente seis planetas e ainda a razão das respectivas distâncias ao Sol. Decidiu por fim que a solução não era numérica mas sim geométrica. Existiam exactamente seis planetas, pensava ele, porque a distância entre cada par adjacente devia estar ligada a um determinado sólido regular, dos quais existem cinco.
    
  Depois de algumas experiências, encontrou um alinhamento de sólidos regulares e de esferas, encaixados uns nos outros, de tal forma que cada um dos seis planetas tinha uma órbita numa das seis esferas: a esfera exterior (em que se desloca Saturno) contém dentro um cubo e, dentro deste, encontra-se, por sua vez, a esfera da órbita de Júpiter. Dentro desta esfera, encontra-se um tetraedro; e Marte desloca-se na esfera que se encontra dentro desse tetraedro. O dodecaedro que se encontra dentro da esfera da órbita de Marte apresenta dentro a esfera correspondente à órbita da Terra, que apresenta no seu interior, um icosaedro dentro do qual se encontra a esfera de Vénus. Por último, o octaedro que se encontra dentro da esfera correspondente à órbita de Vénus contem dentro a esfera da órbita de Mercúrio.

Para ilustrar a sua notável descoberta, Kepler desenhou com todo o cuidado e pormenor a figura reproduzida. Claro que era tudo um disparate!

   Antes do mais, a correspondência entre as esferas encaixadas umas nas outras e as órbitas planetárias não é, de facto, exacta. Tendo sido um dos grandes responsáveis pela apresentação de dados rigorosos sobre as órbitas planetárias, Kepler devia certamente conhecer as discrepâncias existentes. Procurou ainda corrigir o seu modelo utilizando esferas de diferentes espessuras, embora não apresentasse qualquer justificação para essa diferença.

   Em segundo lugar, como sabemos, não existem seis mas, pelo menos, nove planetas. Urano, Neptuno e Plutão, foram descobertos depois de Kepler.

   Porque é que dois gigantes intelectuais como Platão e Kepler teriam defendido teorias tão irrealistas? O que é que os terá levado a procurar ligações entre os sólidos regulares e a estrutura do universo?

   A resposta está no facto de terem partido da mesma profunda convicção que motiva os cientistas actuais: que o padrão e a ordem do mundo podem ser descritos, e em certa medida explicados, através da matemática. Na altura a geometria de Euclides era o ramo da matemática que mais tinha evoluído e, dentro da geometria, a teoria do sólidos regulares ocupava um lugar de destaque; tinha sido conseguida uma classificação completa, na sequência da identificação e dos estudo profundo dos sólidos regulares. Embora a teoria de Kepler não seja defensável, na sua concepção apresentou-se extremanente interessante e muito na linha do ponto de vista expresso pelo seu contemporâneo Galileu:
"O grande livro da Natureza só pode ser lido por aqueles que conhecem a linguagem em que foi escrito. E essa linguagem é a matemática"
   Na verdade, foi a convicção profunda de Kepler na existência de uma ordem matemática que o levou a adoptar o seu modelo matemático de forma a ajustar-se aos dados observados, mantendo a concisão estética do modelo, mesmo à custa de algo que não conseguii explicar.

   A busca da compreensão dos padrões da Natureza através do padrões abstractos da matemática baseou-se numa tradição que ainda hoje continua a dar importantes frutos.




Keith Devlin "Matemática, a ciência do padrões", Porto Editora, 2002



Regresso à página