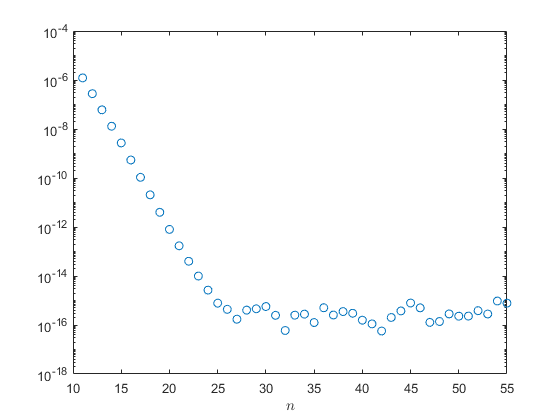
m = 55; A = zeros(m+1, m);

% For all values of degree n.
for n = 10:m
    equation = {@(x,y) cos(x)*diff(y, 2)-sin(x^3-x)*diff(y)+ ...
                  exp(0.5*x^2)*y-cosh(x)*volt(y, @(x,t) sin(x-4*t))+ ...
                  sinh(x)*fred(y, @(x,t) cos(t^2-x)), ...
                @(x) exp(sin(x^3-x)+x^2)};
    domain = [0 1];
    conditions = @(y) {y(0) - 1; y(1)};
    options = tau.settings('degree', n);
    problem = tau.problem(equation, domain, conditions, options);

    % solution via tau method
    [yn, info] = tau.solve(problem);

    % store the coefficients
    A(1:n+1, n) = yn.coeff;
end

% sucessive coefficients of the approximations tend to unchange for
% sufficient large values of n
R = zeros(m-1,1);
for n = 10:m-1
    R(n,1) = norm(A(1:n+1,n)-A(1:n+1,n+1));
end
semilogy(11:55, R(10:m-1,1), 'o')
xlabel('$n$', 'interpreter', 'latex')

Published with MATLAB® R2024a