odeSystem = {@(x,y) cos(x)*diff(y{1})-(x^2-3*x^4)*y{2}+3*diff(y{3}), @(x) cos(x)^2-cos(exp(x))*(-3*x^4+x^2)-6*sin(2*x); ...
@(x,y) sin(x)*diff(y{1})+diff(y{2})-y{3}, @(x) sin(x)*cos(x)-cos(2*x)-sin(exp(x))*exp(x); ...
@(x,y) -y{1}+exp(x)*y{2}+x^3*diff(y{3}), @(x) cos(exp(x))*exp(x)-sin(x)-2*x^3*sin(2*x)};
domain = [-pi pi];
conditions = @(y) {y{1}(-pi); ...
y{2}(0)-cos(1); ...
y{3}(pi)-1};
options = tau.settings('degree', 101);
problem = tau.problem(odeSystem, domain, conditions, options);
yn = tau.solve(problem);
ye = tau.polynomial({@(x) sin(x); @(x) cos(exp(x)); @(x) cos(2*x)}, options);
figure()
subplot(1,2,1)
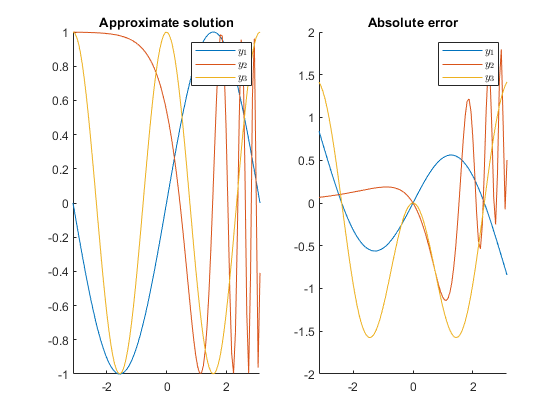
plot(yn)
legend('$y_1$','$y_2$','$y_3$', 'interpreter', 'latex')
title('Approximate solution')
subplot(1,2,2)
plot(yn-ye)
legend('$y_1$','$y_2$','$y_3$', 'interpreter', 'latex')
title('Absolute error')
% % Create tau objects.
% [x, y] = tau('ChebyshevT', [-pi pi], 101);
%
% % Specify problem, conditions and exact solution (if it is known).
% sys = {'cos(x)*diff(y1)-(x^2-3*x^4)*y2+3*diff(y3)=cos(x)^2-cos(exp(x))*(-3*x^4+x^2)-6*sin(2*x)';
% 'sin(x)*diff(y1)+diff(y2)-y3=sin(x)*cos(x)-cos(2*x)-sin(exp(x))*exp(x)';
% '-y1+exp(x)*y2+x^3*diff(y3)=cos(exp(x))*exp(x) - sin(x) - 2*x^3*sin(2*x)'};
% cond = {'y1(-pi)=0';'y2(0)=cos(1)';'y3(pi)=1'};
% es = {'sin(x)';'cos(exp(x))';'cos(2*x)'};
%
% % Solve the problem.
% a = tausolver(x, y, ............................................................% Tau variables.
% sys, ..........................................% System of differential equations.
% cond, ...............................................................% Conditions.
% 'exact_solution', es, ......................................% Solution (optional).
% 'spy', 1); ...............................................% Shows spy of T matrix.