Em 1884, Reuschle imaginou a seguinte resolução mecânica da equação cúbica:
Começou por pôr
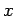 em
evidência no primeiro membro:
em
evidência no primeiro membro: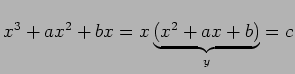
Definindo 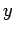 por:
por:
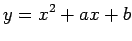
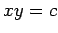
Se completarmos quadrados
em 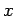 , na
equação do segundo grau
, na
equação do segundo grau
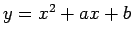 , vem que:
, vem que:
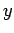 |
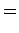 |
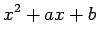 |
|
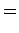 |
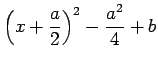 |
(2) |
isto é:
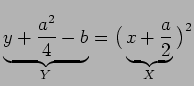
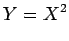
Consideremos um
referencial cartesiano fixo 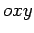 e um outro
móvel
e um outro
móvel 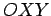 , onde
, onde 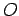 tem
coordenadas
tem
coordenadas
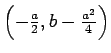 , relativamente ao
referencial fixo.
, relativamente ao
referencial fixo.
As equações (3) exprimem a igualdade vectorial:
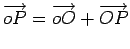 |
(4) |
O vector 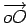 é o vector que translada
a origem
é o vector que translada
a origem 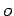 do
referencial fixo para a origem
do
referencial fixo para a origem 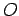 do
referencial móvel.
do
referencial móvel.
Os cálculos
anteriores mostram portanto que a parábola de
equação 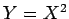 , relativamente ao referencial móvel,
tem,
relativamente
ao referencial fixo, a equação
, relativamente ao referencial móvel,
tem,
relativamente
ao referencial fixo, a equação
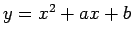 .
.
Podemos então
resolver a equação cúbica (1)
pelo
processo seguinte:
|
No applet seguinte fez-se esta construção para a equação:
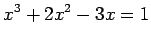
Neste caso
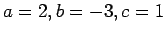 e
e 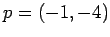 .
.
No applet, pode controlar
com o rato a posição da origem 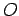 do
referencial móvel (o vértice da parábola),
desenhado na folha
de papel transparente, representada pelo rectângulo côr de
rosa.
Deve fazer coincidir
do
referencial móvel (o vértice da parábola),
desenhado na folha
de papel transparente, representada pelo rectângulo côr de
rosa.
Deve fazer coincidir 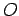 com o ponto
com o ponto 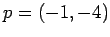 ,
para obter as
raízes da equação dada, isto é as abcissas
dos pontos verdes
no eixo dos
,
para obter as
raízes da equação dada, isto é as abcissas
dos pontos verdes
no eixo dos 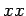 , que
podem ser lidas no applet.
, que
podem ser lidas no applet.
De forma análoga podemos resolver a equação do quarto grau:
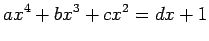
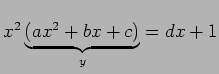
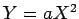 ,
convenientemente transladada, com a hipérbole cúbica
,
convenientemente transladada, com a hipérbole cúbica 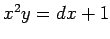 .
.
About this document ...
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html Cubica.tex
The translation was initiated by Joao Nuno Tavares on
2005-04-15
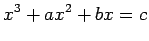
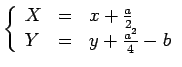
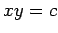 numa
mesa fixa.
numa
mesa fixa. 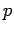 da mesa de coordenadas
da mesa de coordenadas