Construção de Segner
Depois de Descartes numerosos matemáticos interessaram-se pela construção de equações, isto é, pela determinação geométrica (ou gráfica) das raízes de uma equação algébrica.
Em 1761, Johann
Andreas von
Segner propôs uma construção gráfica,
bastante simples,
que permite calcular o valor 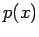 , de uma função
polinomial do tipo:
, de uma função
polinomial do tipo:
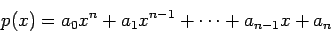
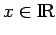 . Esta
construção, que foi
mais tarde popularizada por Lagrange, está esquematizada nas
figuras seguintes:
. Esta
construção, que foi
mais tarde popularizada por Lagrange, está esquematizada nas
figuras seguintes:
Figura 1

Figura 2
- Na recta vertical
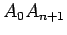 , orientada positivamente
no sentido descendente,
e a partir de uma origem fixa
, orientada positivamente
no sentido descendente,
e a partir de uma origem fixa 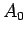 ,
marcámos sucessivamente
pontos
,
marcámos sucessivamente
pontos
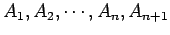 de tal
forma que:
de tal
forma que:
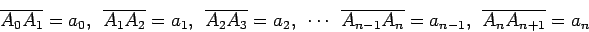
 deve ser
dirigido para baixo se fôr
positivo, e para cima quando fôr negativo.
deve ser
dirigido para baixo se fôr
positivo, e para cima quando fôr negativo. -
Pelo último ponto assim obtido,
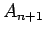 , traçámos uma
recta perpendicular
à
anterior, orientada para a direita, a que chamámos o eixo dos
xx.
Neste eixo, marcámos
o ponto
, traçámos uma
recta perpendicular
à
anterior, orientada para a direita, a que chamámos o eixo dos
xx.
Neste eixo, marcámos
o ponto 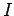 ,
tal que
,
tal que 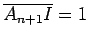 ,
e traçámos uma recta
perpendicular
,
e traçámos uma recta
perpendicular 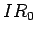 .
O ponto
.
O ponto 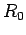 é o ponto
de
intersecção desta recta
com a paralela ao eixo dos xx, que passa
em
é o ponto
de
intersecção desta recta
com a paralela ao eixo dos xx, que passa
em 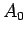 . Unimos ainda o
ponto
. Unimos ainda o
ponto 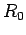 ao ponto
ao ponto 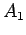 .
. - Finalmente, para obter o valor
de
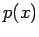 , marcámos
o ponto
, marcámos
o ponto 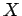 no eixo dos xx,
tal
que
no eixo dos xx,
tal
que 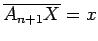 , e
traçámos, por
, e
traçámos, por 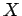 ,
uma recta perpendicular
,
uma recta perpendicular 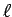 ,
a esse eixo.
Marcámos então o ponto
,
a esse eixo.
Marcámos então o ponto 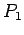 de intersecção
dessa recta com a recta
de intersecção
dessa recta com a recta 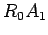 . Por
. Por 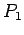 ,
traçámos a paralela ao eixo dos xx, determinámos o
ponto
,
traçámos a paralela ao eixo dos xx, determinámos o
ponto 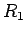 que então
unimos ao
ponto
que então
unimos ao
ponto 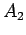 , calculando assim
o ponto
, calculando assim
o ponto 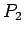 na recta
na recta 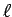 .
Procedendo sucessivamente desta
forma, obtemos uma sucessão de pontos:
.
Procedendo sucessivamente desta
forma, obtemos uma sucessão de pontos:
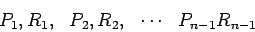
Marcámos por último, a intersecção
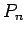 da recta
da recta 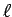 com a recta que une
com a recta que une 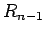 a
a 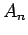 .
O valor de
.
O valor de 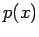 é
então o igual a
é
então o igual a 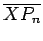 .
.
Animação
da construção
Esta construção está esquematizada na figura 1, e
ilustrada no applet seguinte, onde
podemos constatar que ela continua válida para coeficientes
negativos e para todo o valor de x (positivo, negativo, maior ou menor
que 1).
No applet, que por simplicidade está
construído para uma equação do 3º grau,
podemos modificar os segmentos
 , e o valor
de x, para obter o gráfico de
, e o valor
de x, para obter o gráfico de 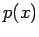 e, em particular, as
raízes da equação
e, em particular, as
raízes da equação 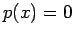 .
.
Justificação teórica da construção
Para proceder à prova de
que, de facto, 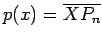 ,
desenhámos na figura 2, as
rectas auxiliares, paralelas ao eixo dos xx, que passam nos pontos
,
desenhámos na figura 2, as
rectas auxiliares, paralelas ao eixo dos xx, que passam nos pontos 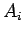 , o que permite
determinar os pontos
, o que permite
determinar os pontos 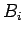 na recta
na recta 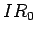 . Consideremos ainda os
comprimentos seguintes:
. Consideremos ainda os
comprimentos seguintes:
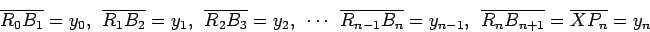
e o par de triângulos semelhantes I e II, representados na figura 2. Daí concluímos que:
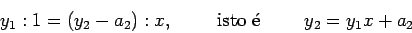
e, procedendo de forma análoga relativamente aos outros pares de triângulos semelhantes , obtemos as equações:
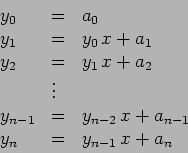
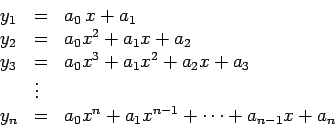
o que termina a demonstração do método de Segner.
Aparelho de Rowning
A construção de Segner foi realizada materialmente no seguinte aparelho de Rowning (Philos. Trans. London Math. Soc. 60 (1770)):

