| Next: Aparelhos para construir cónicas. Previous: Compasso perfeito Contents | ||||
|
|
||||
Para uma exploração interactiva deste teorema, com
excelentes applets, veja a página "Modelos computacionais na prova
Matemática" da autoria de Marta Brandão.
De seguida apresentamos uma prova formal deste teorema. |
||||
Por outro lado, como
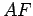 e e 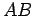 são ambas tangentes à
esfera de centro são ambas tangentes à
esfera de centro  , temos , temos 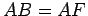 . De forma análoga, . De forma análoga, 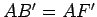 ,
e ainda: ,
e ainda:
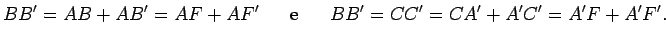 Resulta daí que: 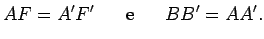 A curva obtida, lugar
geométrico dos pontos Se traçarmos 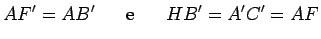
Os planos que
contêm os paralelos
Se tomarmos agora o
paralelo 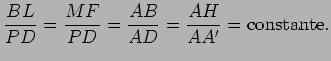 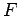 e á
recta e á
recta 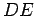 estão entre si numa
razão constante, o que mostra que
a recta estão entre si numa
razão constante, o que mostra que
a recta 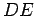 é uma das directrizes da
elipse e a constante
referida a respectiva excentricidade. A mesma
demonstração
aplica-se ao foco é uma das directrizes da
elipse e a constante
referida a respectiva excentricidade. A mesma
demonstração
aplica-se ao foco 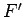 e á recta e á recta 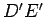 . As rectas . As rectas 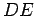 , , 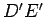 ,
são pois as directrizes da elipse. ,
são pois as directrizes da elipse. |
||||
|
||||
Por outro lado, a
intersecção do plano secante e do paralelo 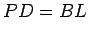
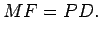 A curva obtida é
pois uma parábola cujo foco é o ponto |
||||
|
|
||||
| Next: Aparelhos para construir cónicas. Previous: Compasso perfeito Contents |

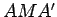 .
. 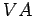 e
e 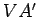 e o plano secante segundo a recta
e o plano secante segundo a recta 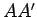 .
. 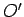 , respectivamente, a primeira acima de
, respectivamente, a primeira acima de 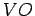 , estas duas
circunferências irão gerar duas esferas, tangentes
á
superfície cónica segundo os paralelos
, estas duas
circunferências irão gerar duas esferas, tangentes
á
superfície cónica segundo os paralelos 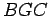 e
e 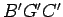 , e
tangentes ainda ao plano secante nos pontos
, e
tangentes ainda ao plano secante nos pontos 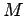 qualquer sobre a curva de
intersecção do plano secante com o cone; tomemos as
rectas
qualquer sobre a curva de
intersecção do plano secante com o cone; tomemos as
rectas 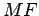 ,
, 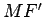 e a geratriz
e a geratriz 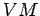 que intersectará, em
que intersectará, em 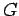 e em
e em 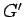 , os
paralelos
, os
paralelos 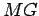 são ambas tangentes à esfera de
centro
são ambas tangentes à esfera de
centro 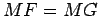 . Anàlogamente, como as rectas
. Anàlogamente, como as rectas 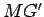 são ambas tangentes
à esfera de centro
são ambas tangentes
à esfera de centro  . Portanto:
. Portanto: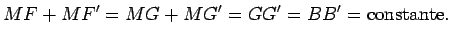
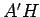 paralela a
paralela a 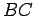 ,
, 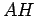 é a
distância focal desta elipse. Com efeito,
é a
distância focal desta elipse. Com efeito,
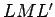 do cone (não
representado na figura), a sua intersecção com o plano
secante é o
segmento
do cone (não
representado na figura), a sua intersecção com o plano
secante é o
segmento 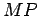 , que é perpendicular ao
eixo maior
, que é perpendicular ao
eixo maior 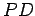 . Mas os triângulos
. Mas os triângulos
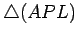 ,
,
 e
e
 ,
são
semelhantes, e daí que:
,
são
semelhantes, e daí que:

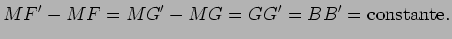
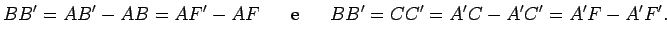
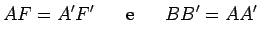
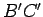 ,
, 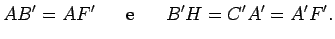
![$ [LVL']$](img65.png) perpendicular
ao plano secante.
Este último é paralelo á geratriz
perpendicular
ao plano secante.
Este último é paralelo á geratriz 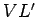 e é intersectado
pelo plano meridiano segundo a recta
e é intersectado
pelo plano meridiano segundo a recta 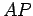 , paralela a essa geratriz.
, paralela a essa geratriz. 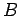 e em
e em 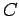 , e à recta
, e à recta 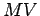 , são ambas tangentes à esfera
em
, são ambas tangentes à esfera
em 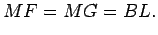

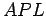 e
e 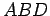 são ambos isósceles, uma vez que
são ambos semelhantes ao triângulo
são ambos isósceles, uma vez que
são ambos semelhantes ao triângulo 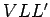 . Por isso, tem-se que:
. Por isso, tem-se que: