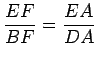III.2. Conicógrafo de Artobolevskii

Este aparelho mecaniza a definição 3.1, da
secção III. O ponto 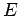 gera uma cónica. Deverá ter-se
gera uma cónica. Deverá ter-se 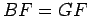 ; o segmento
; o segmento
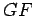 é determinado pela
condição:
é determinado pela
condição:
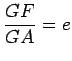
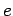 é a excentricidade da
curva. A barra
é a excentricidade da
curva. A barra 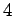 deve mover-se
paralelamente à directriz
deve mover-se
paralelamente à directriz 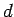 .
.
Da semelhança dos
triângulos 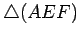 e
e
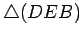 ,
concluímos que:
,
concluímos que:
Consideremos a
perependicular de 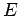 para
para 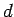 e seja
e seja 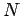 a
intersecção desta perpendicular com a recta
a
intersecção desta perpendicular com a recta 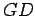 .
.
Da semelhança dos
triângulos 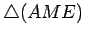 e
e
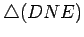 ,
concluímos que:
,
concluímos que:
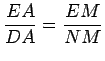
Atendendo a (6), vem finalmente que:
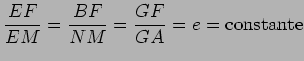
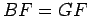 e
e 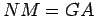 .
.
O ponto 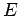 descreve pois uma cónica de foco
descreve pois uma cónica de foco 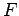 e directriz
e directriz 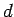 .
Como sabemos, se
.
Como sabemos, se 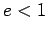 a cónica
será uma elipse, se
a cónica
será uma elipse, se 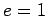 uma
parábola e se
uma
parábola e se 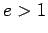 uma hipérbole.
Podemos ajustar as dimenões
das componentes do mecanismo (mesmo no applet) para obter cada um
dos três tipos de cónica.
uma hipérbole.
Podemos ajustar as dimenões
das componentes do mecanismo (mesmo no applet) para obter cada um
dos três tipos de cónica.