Vânia Oliveira e Inês Cruz 2
O problema dos três corpos (com força de atracção Newtoniana)
é o estudo do movimento de três corpos de massas arbitrárias, ![]() e
e
![]() , em movimento por acção exclusiva da força de atracção Newtoniana
entre cada par de corpos.
, em movimento por acção exclusiva da força de atracção Newtoniana
entre cada par de corpos.
Este problema surge naturalmente no estudo do movimento dos planetas. Por exemplo o sistema Sol-Terra-Lua pode considerar-se como um caso particular do problema dos três corpos se desprezarmos o efeitos dos outros planetas neste sistema. Também o sistema Terra-Lua-satélite constitui um caso particular deste problema desprezando o efeito exercido pelo Sol e pelos outros planetas no sistema. Este último problema é, no entanto, tratado de forma mais conveniente se considerarmos que o satélite tem massa nula quando comparada com as massas da Terra e da Lua, enquadrando-se melhor no chamado problema restrito dos três corpos.
É costume distinguir o problema geral dos três corpos (em que os corpos se movem no espaço tridimensional) do problema planar dos três corpos (os corpos movem-se num mesmo plano ao longo do tempo).
O problema pode definir-se para um número ![]() arbitrário de corpos,
chamando-se então o problema dos
arbitrário de corpos,
chamando-se então o problema dos ![]() corpos, e constitui um
dos desafios que, tendo interessado matemáticos eminentes ao longo
dos séculos, continua por resolver.
corpos, e constitui um
dos desafios que, tendo interessado matemáticos eminentes ao longo
dos séculos, continua por resolver.
O que significa exactamente resolver o problema dos ![]() corpos?
Na sua interpretação clássica resolver o problema consiste em obter
uma expressão para a posição de cada corpo num instante
corpos?
Na sua interpretação clássica resolver o problema consiste em obter
uma expressão para a posição de cada corpo num instante ![]() arbitrário,
dadas as massas dos
arbitrário,
dadas as massas dos ![]() corpos e as suas posições e velocidades num
instante inicial
corpos e as suas posições e velocidades num
instante inicial ![]() .
.
Neste sentido clássico o problema só está resolvido no caso ![]() e, mesmo neste caso simples, a expressão para a posição dos corpos
num instante
e, mesmo neste caso simples, a expressão para a posição dos corpos
num instante ![]() arbitrário envolve integrais cuja expressão analítica
não é conhecida.
arbitrário envolve integrais cuja expressão analítica
não é conhecida.
No caso ![]() conhecem-se algumas soluções clássicas (soluções
no sentido clássico). Tais soluções existem para três corpos de massas
arbitrárias mas com posições e velocidades iniciais devidamente escolhidas.
Elas podem ser divididas em dois tipos (soluções colineares
e soluções equiláteras) e foram obtidas respectivamente por
EULER (1772) e por LAGRANGE (1772).
conhecem-se algumas soluções clássicas (soluções
no sentido clássico). Tais soluções existem para três corpos de massas
arbitrárias mas com posições e velocidades iniciais devidamente escolhidas.
Elas podem ser divididas em dois tipos (soluções colineares
e soluções equiláteras) e foram obtidas respectivamente por
EULER (1772) e por LAGRANGE (1772).
Muito recentemente MONTGOMERY (2000) obteve uma nova solução no caso dos três corpos terem massas iguais (figura oito) usando métodos variacionais.
Importa notar que todas estas soluções são soluções do problema planar dos três corpos.
Em alguns casos é possível obter o desenho das órbitas dos três corpos, ou melhor, o desenho do seu percurso ao longo do tempo, sem obter uma solução no sentido clássico. A este desenho chamaremos solução geométrica do problema dos três corpos. Uma solução geométrica está para a respectiva solução clássica como a imagem de uma curva está para a expressão da curva. Em particular a solução geométrica ``ignora'' a velocidade com que a solução clássica é percorrida e o modo como é percorrida.
Por exemplo, nas soluções colineares (de EULER) os três corpos mantêm-se sempre colineares, e as soluções geométricas são constituídas por três cónicas semelhantes ou por três semirectas. Nas soluções equiláteras (de LAGRANGE) os três corpos encontram-se sempre nos vértices de um triângulo equilátero e as soluções geométricas são novamente constituídas por três cónicas semelhantes ou por três semirectas.
Na realidade as soluções geométricas de Euler e de Lagrange não ``ignoram'' totalmente o modo como a curva é percorrida. Elas ``sabem'' que os corpos nunca invertem o sentido do movimento em torno de um dos focos da cónica e que as suas velocidades angulares são maiores quando os corpos estão mais perto desse foco (consequências da Segunda Lei de KEPLER - ver apêndice A).
Para formularmos as equações diferenciais que regulam o movimento
dos três corpos comecemos por introduzir algumas notações.
Designemos por ![]() e
e ![]() as massas dos três corpos
e por
as massas dos três corpos
e por ![]() um ponto arbitrário do espaço onde os corpos se movem.
Denotemos por
um ponto arbitrário do espaço onde os corpos se movem.
Denotemos por
![]() e
e
![]() os vectores de posição dos corpos em
os vectores de posição dos corpos em ![]() no instante
no instante ![]() . Então
a força de atracção Newtoniana exercida no corpo
. Então
a força de atracção Newtoniana exercida no corpo ![]() pelo corpo
pelo corpo ![]() é:
é:
onde ![]() designa a distância entre os corpos,
designa a distância entre os corpos, ![]() é
o versor da recta que os une dirigido do corpo
é
o versor da recta que os une dirigido do corpo ![]() para
o corpo
para
o corpo ![]() e
e ![]() é a constante de gravitação universal. A força exercida no corpo
é a constante de gravitação universal. A força exercida no corpo ![]() pelo corpo
pelo corpo ![]() é
é ![]() .
.
Assumiremos que os corpos nunca chocam, ou seja, que em qualquer instante
![]() teremos sempre
teremos sempre ![]() , para
, para ![]() .
.
A segunda lei de Newton afirma que as equações diferenciais satisfeitas
pelos vectores
![]() são:
são:
Se pretendermos estudar o problema planar dos três corpos então cada
um dos vectores
![]() terá somente duas coordenadas e
teremos seis equações diferenciais para o movimento.
terá somente duas coordenadas e
teremos seis equações diferenciais para o movimento.
O centro de massa do sistema dos três corpos é o ponto ![]() cujo vector
de posição em
cujo vector
de posição em ![]() é:
é:
Obviamente o centro de massa do sistema não depende da escolha do
ponto ![]() . Além disso o centro de massa do sistema tem movimento
rectilíneo e uniforme (basta somar as três equações diferenciais vectoriais
em (1)).
. Além disso o centro de massa do sistema tem movimento
rectilíneo e uniforme (basta somar as três equações diferenciais vectoriais
em (1)).
Podemos então assumir que o centro de massa do sistema dos três corpos
está ``parado'' e tomá-lo para origem ![]() do referencial. Com
esta escolha da origem teremos sempre a identidade:
do referencial. Com
esta escolha da origem teremos sempre a identidade:
Consideremos as novas variáveis:
Por outras palavras ![]() é o vector que une os corpos 2 e
3 (aplicado em
é o vector que une os corpos 2 e
3 (aplicado em ![]() ),
), ![]() é o vector que une os corpos
3 e 1 e
é o vector que une os corpos
3 e 1 e ![]() é o vector que une os corpos 1 e 2.
é o vector que une os corpos 1 e 2.
Facilmente se conclui que:
e que os vectores ![]() se obtêm dos vectores
se obtêm dos vectores ![]() pelas relações:
pelas relações:
onde
![]() é o que chamaremos de massa
total. Além disso, nas variáveis
é o que chamaremos de massa
total. Além disso, nas variáveis
![]() e
e
![]() as equações (1) são simplesmente:
as equações (1) são simplesmente:
onde ![]() é a norma de
é a norma de ![]() e:
e:
As equações (5) formam um conjunto de nove equações diferenciais de segunda ordem.
No tratamento do problema planar dos três corpos teremos apenas seis
equações diferenciais já que que cada ![]() terá somente
duas coordenadas. As soluções que descreveremos adiante serão soluções
do problema planar.
terá somente
duas coordenadas. As soluções que descreveremos adiante serão soluções
do problema planar.
A ideia de EULER foi procurar soluções das equações diferenciais (1) para as quais os corpos se mantivessem sempre colineares.
Em termos dos vectores ![]() procuremos então soluções colineares
das equações (5). Permutando se necessário os índices 1,
2 e 3, podemos assumir que o terceiro corpo está entre o primeiro
e o segundo (note-se que estamos a assumir a não existência de choques). Neste caso procuramos soluções de (5) da forma:
procuremos então soluções colineares
das equações (5). Permutando se necessário os índices 1,
2 e 3, podemos assumir que o terceiro corpo está entre o primeiro
e o segundo (note-se que estamos a assumir a não existência de choques). Neste caso procuramos soluções de (5) da forma:
onde ![]() é uma função positiva de
é uma função positiva de ![]() .
.
Derivando a segunda equação de (7) duas vezes, substituindo na segunda equação de (5) e comparando com a primeira daquelas equações conclui-se que deverá ter lugar a seguinte igualdade:
A igualdade (8) por sua vez implica uma de duas igualdades:
ou
Assumamos de momento que a primeira destas igualdades não se verifica. Em tal caso deverá verificar-se a segunda igualdade pelo que o vector ![]() é necessariamente da forma:
é necessariamente da forma:
Substituindo em (4) para recuperar os vectores de posição ![]() , facilmente se conclui que (9) implica que os três corpos se movem sempre sobre a mesma recta.
, facilmente se conclui que (9) implica que os três corpos se movem sempre sobre a mesma recta.
Passemos então às soluções colineares das equações (5) para as quais ![]() é constante. São estas soluções que são conhecidas por soluções de EULER.
Teremos então:
é constante. São estas soluções que são conhecidas por soluções de EULER.
Teremos então:
Sendo ![]() e
e ![]() o polinómio tem certamente uma raíz
positiva. A unicidade da raíz positiva resulta da regra de sinais
de DESCARTES que se pode encontrar por exemplo em:
o polinómio tem certamente uma raíz
positiva. A unicidade da raíz positiva resulta da regra de sinais
de DESCARTES que se pode encontrar por exemplo em:
Notemos que a referida raíz positiva existe e é única quaisquer
que sejam os números positivos ![]() e
e ![]() .
.
Nota: Verifica-se facilmente que
![]() . Assim, se
. Assim, se ![]() então
então
![]() , i.e.,
, i.e., ![]() é a única raíz positiva de
é a única raíz positiva de ![]() .
Neste caso, fazendo uso das equações (4), conclui-se facilmente
que o terceiro corpo coincide com o centro de massa do sistema, mantendo-se
pois ``parado'' durante todo o tempo.
.
Neste caso, fazendo uso das equações (4), conclui-se facilmente
que o terceiro corpo coincide com o centro de massa do sistema, mantendo-se
pois ``parado'' durante todo o tempo.
Tendo concluído que ![]() tem necessariamente uma raíz positiva
podemos regressar às equações (5). Multiplicando a primeira destas
equações por
tem necessariamente uma raíz positiva
podemos regressar às equações (5). Multiplicando a primeira destas
equações por ![]() , a terceira por
, a terceira por ![]() , subtraindo e usando (10), obtemos
a equação diferencial a ser satisfeita por
, subtraindo e usando (10), obtemos
a equação diferencial a ser satisfeita por
![]()
Esta equação diferencial descreve o movimento de um corpo de massa
1 no problema de KEPLER (ver apêndice A).
As soluções geométricas deste problema são bem conhecidas e classificam-se,
em função da energia total ![]() e do vector momento angular
e do vector momento angular
![]() de (12), em:
de (12), em:
A semirecta tem origem em ![]() e cada uma destas cónicas tem um foco em
e cada uma destas cónicas tem um foco em ![]() .
.
Concluiu-se que, dados três corpos de massas arbitrárias ![]() ,
,
![]() e
e ![]() , existe um único número positivo
, existe um único número positivo ![]() tal
que, para qualquer solução
tal
que, para qualquer solução
![]() do problema de KEPLER,
se tem que:
do problema de KEPLER,
se tem que:
satisfazem as equações (5). Usando (4) para recuperar os vectores ![]() obtêm-se soluções colineares do problema dos três corpos ou, equivalentemente,
de (1).
obtêm-se soluções colineares do problema dos três corpos ou, equivalentemente,
de (1).
As três animações que apresentamos a seguir foram obtidas com:
A título de curiosidade incluimos também a animação obtida quando ![]() (o
que dá
(o
que dá ![]() ) e com movimento elíptico de
) e com movimento elíptico de ![]() . Como
previsto o terceiro corpo mantém-se parado durante o processo.
. Como
previsto o terceiro corpo mantém-se parado durante o processo.
Procuremos agora soluções de (5) que verificam
![]() em qualquer instante
em qualquer instante ![]() . Usando a identidade (3) juntamente
com a propriedade pretendida facilmente se conclui que tem necessariamente lugar uma das duas afirmações:
. Usando a identidade (3) juntamente
com a propriedade pretendida facilmente se conclui que tem necessariamente lugar uma das duas afirmações:
As soluções (que verificaremos existirem!) satisfazendo a segunda destas condições, serão chamadas de soluções equiláteras e foram descobertas por LAGRANGE.
Tal condição indica precisamente que, em cada instante, os três
corpos se situam sobre os vértices de um triângulo equilátero. Tal
triângulo, no entanto, varia com ![]() em tamanho e posição.
em tamanho e posição.
Na realidade é surpreendentemente fácil mostrar que existem soluções equiláteras. Pela própria condição de equilateralidade as equações (5) reduzem-se a três problemas de KEPLER ``iguais'':
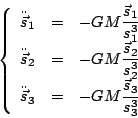
Estes três problemas de KEPLER, aparentemente independentes,
são na realidade dependentes por via da condição de equilateralidade.
De facto, conhecido
![]() , necessariamente
, necessariamente
![]() e
e
![]() se obtêm de
se obtêm de
![]() rodando, respectivamente,
de
rodando, respectivamente,
de ![]() e
e ![]() em torno de
em torno de ![]() .
.
Concluiu-se então que, dados três corpos de massas arbitrárias ![]() e
e ![]() , e uma solução arbitrária
, e uma solução arbitrária
![]() do
problema de KEPLER, os vectores
do
problema de KEPLER, os vectores
![]() e
e
![]() que se obtêm de
que se obtêm de
![]() rodando, respectivamente, de
rodando, respectivamente, de ![]() e
e ![]() em torno de
em torno de ![]() , constituem, juntamente com
, constituem, juntamente com
![]() uma solução de (5) com a propriedade
uma solução de (5) com a propriedade
![]() .
.
Para cada uma destas soluções de (5) recuperamos os vectores
![]() através de (4) e obtemos uma solução equilátera
do problema dos três corpos.
através de (4) e obtemos uma solução equilátera
do problema dos três corpos.
Seguem-se duas animações destas soluções no caso da razão das massas
ser
![]() , e
, e ![]() descrever, respectivamente,
uma elipse e uma parábola. Novamente cada um dos três corpos descreve uma cónica sendo o centro de massa do sistema o foco comum das três cónicas.
descrever, respectivamente,
uma elipse e uma parábola. Novamente cada um dos três corpos descreve uma cónica sendo o centro de massa do sistema o foco comum das três cónicas.
Chama-se coreografia do problema dos três corpos a uma solução do problema dos três corpos tal que os três corpos se movimentam sobre uma mesma curva plana (curva base), sem choques.
A título de exemplo, e usando as soluções de LAGRANGE, consideremos
a animação obtida com
![]() e uma solução geométrica circular
e uma solução geométrica circular
![]() do problema de KEPLER.
Obtemos claramente uma coreografia dos três corpos em que a curva
base é uma circunferência.
do problema de KEPLER.
Obtemos claramente uma coreografia dos três corpos em que a curva
base é uma circunferência.
A solução de MONTGOMERY, cuja existência foi estabelecida
por métodos variacionais, é também uma coreografia e foi obtida
também para o caso de massas iguais:
![]() . A curva
base desta coreografia é a chamada figura oito, cujo gráfico
é análogo ao símbolo
. A curva
base desta coreografia é a chamada figura oito, cujo gráfico
é análogo ao símbolo ![]() . Animações desta coreografia podem
ser visualisadas por exemplo em:
. Animações desta coreografia podem
ser visualisadas por exemplo em:
Neste apêndice pretendemos estudar as soluções geométricas do problema
de KEPLER. Este problema pode ser descrito como o estudo
do movimento de um corpo de massa ![]() sobre o qual actua uma
força de atracção Newtoniana.
sobre o qual actua uma
força de atracção Newtoniana.
Por exemplo este é o problema associado ao movimento de um planeta em torno do Sol se desprezarmos o efeito dos outros planetas sobre ele. É também o caso do movimento de um satélite em órbita em torno da Terra se desprezarmos o efeito da Lua sobre ele.
Escolhendo para origem do sistema de coordenadas, ![]() , o centro
de atracção (o centro do Sol ou o centro da Terra nos exemplos citados)
e denotando por
, o centro
de atracção (o centro do Sol ou o centro da Terra nos exemplos citados)
e denotando por ![]() o vector de posição do corpo de massa
o vector de posição do corpo de massa
![]() em relação a
em relação a ![]() , a segunda lei de Newton dá-nos a equação
diferencial satisfeita por
, a segunda lei de Newton dá-nos a equação
diferencial satisfeita por ![]() :
:
onde ![]() é um número real positivo,
é um número real positivo, ![]() é a distância
do corpo a
é a distância
do corpo a ![]() e
e ![]() é o versor da direcção
é o versor da direcção ![]() dirigido de
dirigido de ![]() para o corpo. Nos exemplos acima citados a constante
para o corpo. Nos exemplos acima citados a constante
![]() toma o valor
toma o valor ![]() , onde
, onde ![]() é a constante de gravitação universal
e
é a constante de gravitação universal
e ![]() é a massa do Sol ou da Terra.
é a massa do Sol ou da Terra.
Na realidade prova-se facilmente que o movimento do corpo tem sempre
lugar num plano que contém ![]() . Esta é a primeira consequência da
chamada Lei de Conservação do Momento Cinético (ou Angular),
cujo enunciado é o seguinte:
. Esta é a primeira consequência da
chamada Lei de Conservação do Momento Cinético (ou Angular),
cujo enunciado é o seguinte:
Ao vector ![]() chama-se vector momento cinético do sistema. Esta lei de conservação tem duas consequências importantes:
chama-se vector momento cinético do sistema. Esta lei de conservação tem duas consequências importantes:
Nota: A quantidade ![]() coincide com a norma de
coincide com a norma de ![]() se
se
![]() e com o seu simétrico se
e com o seu simétrico se
![]() .
.
A segunda consequência é geralmente conhecida como Segunda Lei de KEPLER e garante que:
A segunda lei de conservação, a Lei de Conservação da Energia,
permite, em conjunto com a Segunda Lei de KEPLER,
obter uma relação entre as coordenadas ![]() e
e ![]() , conduzindo
assim às soluções geométricas do problema de KEPLER.
, conduzindo
assim às soluções geométricas do problema de KEPLER.
À função ![]() chama-se energia total do sistema.
chama-se energia total do sistema.
Combinando a Lei de Conservação da Energia com a Segunda Lei de KEPLER obtem-se facilmente a seguinte relação:
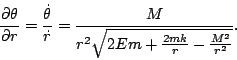
Integrando em ordem a ![]() obtem-se a relação pretendida:
obtem-se a relação pretendida:
onde
![]() e
e
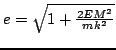 .
.
Recordemos que, se ![]() então o corpo move-se numa semirecta passando por
então o corpo move-se numa semirecta passando por ![]() .
.
Se ![]() então a relação (14) reescreve-se como:
então a relação (14) reescreve-se como:
que é precisamente a equação focal de uma cónica de parâmetro
![]() e excentricidade
e excentricidade ![]() . Por outras palavras, o corpo descreve
uma cónica em que um dos focos é o ponto
. Por outras palavras, o corpo descreve
uma cónica em que um dos focos é o ponto ![]() . Tal cónica será uma:
. Tal cónica será uma: