 |
-4- | |
Espelhos matriciais
|
menu |
| O PCA O PCA
(Principal
Component
Analysis) procura as direcções de variância
máxima da informação. A direcção do
primeiro componente será calculada como a direcção
onde a variância das projecções dos vectores
calculados a partir de todos os retratos é máxima e assim
sucessivamente, em direcções ortognais. A Figura 4
permite observar o PCA num caso simples 2D.
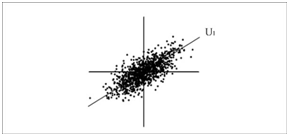 Figura 4 No
conjunto de
dados 2D
representados, o 1º eixo PCA escolhido seria o eixo U1. É
fácil perceber que se pretendêssemos substituir cada um
dos vectores 2D, associados a cada ponto, por um só componente,
esta solução minimizaria o erro. O PCA permite
reconstruir os dados com erros pequenos, com um mínimo de
componentes
As técnicas de PCA permitem portanto encontrar, para uma variável vectorial X, uma matriz construída com todos os vectores imagem, um novo sistema de eixos ortogonais, que permitem decompor cada um desses vectores numa série optimizada de componentes, construídos sobre cada um desses eixos. O ICA utiliza um critério diferente, procurando identificar direcções que correspondam a comportamentos não gaussianos, acreditando que dessa forma, ao identificar variáveis independentes, será capaz de encontrar dados “interessantes”. Como simples ilustração destas técnicas de decomposição factorial poder-se-ia utilizar a decomposição de um sinal numa série de Fourier, onde cada componente da série corresponde de facto a um coeficiente num eixo de um sistema de eixos ortogonais. |
| Espelhos matriciais - Galeria >>>> | <<anterior | seguinte>> | |
| CMUP - Arte e Matemática |