|
Consideremos dois planos  e e  , a que chamamos plano
móvel e fixo,
respectivamente, e imaginemos que , a que chamamos plano
móvel e fixo,
respectivamente, e imaginemos que  se desloca
sobre se desloca
sobre  . .
Mais sugestivamente, imaginemos que o plano
 é o plano de
uma
mesa e que é o plano de
uma
mesa e que  é uma placa plana de
plástico (transparente)
indeformável que deslocamos sobre a mesa. Nos instantes é uma placa plana de
plástico (transparente)
indeformável que deslocamos sobre a mesa. Nos instantes
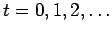 a placa a placa
 ocupará
determinadas
posições
sobre ocupará
determinadas
posições
sobre  , que designamos sucessivamente por , que designamos sucessivamente por
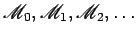 . .
Pontos e rectas de  serão designados por letras
latinas
maiúsculas serão designados por letras
latinas
maiúsculas 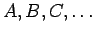 e minúsculas e minúsculas
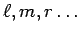 ,
respectivamente. No movimento de ,
respectivamente. No movimento de  sobre sobre  um ponto um ponto
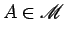 ocupará
sucessivamente as posições ocupará
sucessivamente as posições
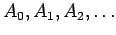 em em
 , uma recta , uma recta  de de  ocupará
sucessivamente as posições ocupará
sucessivamente as posições
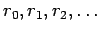 em em
 , e
anàlogamente para qualquer outra figura de , e
anàlogamente para qualquer outra figura de
 . .
Pontos e rectas fixas de  serão designados por letras
latinas
minúsculas serão designados por letras
latinas
minúsculas 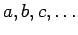 e por letras gregas e por letras gregas
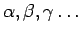 ,
respectivamente. O movimento de ,
respectivamente. O movimento de  sobre sobre
 , será representado pela
notação , será representado pela
notação  . .
Na figura seguinte ilustramos o que acabamos de referir,
representando, para maior clareza de exposição, o plano
 por
um rectângulo limitado amarelo, transportando consigo um ponto por
um rectângulo limitado amarelo, transportando consigo um ponto 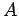 , uma recta , uma recta  e uma estrela e uma estrela 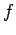 . O plano . O plano
 é o plano
vermelho. é o plano
vermelho.

|
|
|
Durante este movimento, ambos os planos se mantêm
indeformáveis,
isto é, as distâncias entre os pontos de cada um
mantêm-se
inalteradas. Sendo assim, não é difícil mostrar
que esse
movimento fica completamente determinado conhecendo o movimento de
dois quaisquer dos pontos de  . .
Consideremos então dois pontos
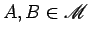 que, para duas
posições sucessivas arbitrárias de
que, para duas
posições sucessivas arbitrárias de
 em em
 , ocupam as
posições , ocupam as
posições 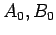 e e 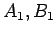 , em , em
 , como na figura
seguinte: , como na figura
seguinte:
|
|
|
Através do ponto médio do segmento  traçamos a
perpendicular a este segmento, e, anàlogamente, através
do
ponto médio do segmento 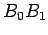 a respectiva perpendicular.
Seja 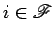 o ponto de
encontro destas duas perpendiculares.
Temos então que (porquê?):
Os triângulos 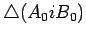 e e
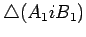 são pois
iguais e daí que: são pois
iguais e daí que:
Vemos portanto que, por
uma rotação em torno de  , o ponto , o ponto  será
transformado em será
transformado em 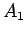 e simultâneamente, e simultâneamente, 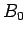 em em  . Como a
posição de . Como a
posição de  em em  fica completamente
determinada pelas posições de dois dos seus pontos,
concluímos que: fica completamente
determinada pelas posições de dois dos seus pontos,
concluímos que:
O
movimento de  em em  , da posição , da posição
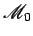 para
a
posição para
a
posição 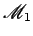 pode ser obtido por
uma rotação em torno de um
certo ponto fixo pode ser obtido por
uma rotação em torno de um
certo ponto fixo 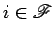 , que se chama por
isso, o centro de
rotação. , que se chama por
isso, o centro de
rotação. |
O que acabamos de dizer
é independente das posições de
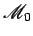 e e
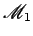 . Se
estas
posições se tornam infinitamente
próximas, obtemos resultados aplicáveis a cada instante
do
movimento contínuo de . Se
estas
posições se tornam infinitamente
próximas, obtemos resultados aplicáveis a cada instante
do
movimento contínuo de  sobre sobre  . A corda . A corda  converge então para a
tangente à trajectória de converge então para a
tangente à trajectória de 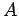 , e a normal a essa corda, através do seu
ponto médio, converge para a normal à trajectória
de , e a normal a essa corda, através do seu
ponto médio, converge para a normal à trajectória
de 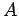 que passa em que passa em 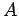 . Portanto: . Portanto:
Quando um plano  se
desloca continuamente sobre um
plano se
desloca continuamente sobre um
plano  , as normais às
trajectórias de todos os seus pontos
passam, em cada instante, por um mesmo ponto. O sistema executa nesse
instante uma rotação infinitesimal em
torno desse ponto que, por isso, se chama o centro instantâneo de
rotação. , as normais às
trajectórias de todos os seus pontos
passam, em cada instante, por um mesmo ponto. O sistema executa nesse
instante uma rotação infinitesimal em
torno desse ponto que, por isso, se chama o centro instantâneo de
rotação.
|
Para além das
trajectórias dos pontos de  , é importante
estudar a envolvente, no plano fixo, das diversas
posições que
uma recta (ou uma outra qualquer curva) de , é importante
estudar a envolvente, no plano fixo, das diversas
posições que
uma recta (ou uma outra qualquer curva) de
 ocupa, quando ocupa, quando
 se move sobre se move sobre
 . Aqui o resultado
essencial é
o seguinte: . Aqui o resultado
essencial é
o seguinte:
Quando um plano  se desloca continuamente sobre um
plano se desloca continuamente sobre um
plano  , as normais às envolventes das
rectas (e outras
curvas) de , as normais às envolventes das
rectas (e outras
curvas) de  ,
nos pontos de contacto (pontos característicos) com essas rectas
(ou
curvas), passam todas pelo centro instantâneo de
rotação. Esses pontos
de contacto chamam-se pontos
característicos da linha considerada. ,
nos pontos de contacto (pontos característicos) com essas rectas
(ou
curvas), passam todas pelo centro instantâneo de
rotação. Esses pontos
de contacto chamam-se pontos
característicos da linha considerada. |
Por outras palavras: o
ponto em que (a posição de) uma recta
de  , num certo instante, toca a sua
envolvente em , num certo instante, toca a sua
envolvente em  , é o pé da
perpendicular baixada do centro instantâneo de
rotação sobre essa
recta. , é o pé da
perpendicular baixada do centro instantâneo de
rotação sobre essa
recta.
Vamos ver que, de facto,
assim é. Para determinar o ponto
característico, onde uma recta móvel 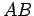 toca, numa das suas
posições, a curva envolvente das suas sucessivas
posições em toca, numa das suas
posições, a curva envolvente das suas sucessivas
posições em
 , consideremos uma
posição muito próxima , consideremos uma
posição muito próxima 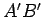 dessa
recta. Suponhamos que estas duas rectas, se intersectam num ponto dessa
recta. Suponhamos que estas duas rectas, se intersectam num ponto 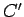 de
de 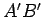 , e seja , e seja 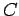 o ponto de o ponto de 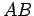 que corresponde ao ponto que corresponde ao ponto 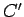 . .
|
|
|
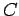 varia sobre varia sobre 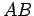 ao mesmo que tempo que ao mesmo que tempo que 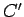 varia sobre varia sobre 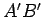 e, no limite, quando e, no limite, quando 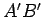 se justapõe a se justapõe a 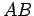 , ambos os
pontos convergem para o mesmo ponto de , ambos os
pontos convergem para o mesmo ponto de 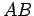 , que é exactamente o
ponto característico de , que é exactamente o
ponto característico de 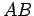 . .
Mas, como sabemos, as perpendiculares aos segmentos 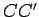 , que
passam nos respectivos pontos médios, passam todas pelo centro
de
rotação , que
passam nos respectivos pontos médios, passam todas pelo centro
de
rotação  . Por outro lado, as rectas . Por outro lado, as rectas  e e 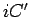 são normais
às trajectórias desses pontos. Portanto no limite, a
normal à
recta são normais
às trajectórias desses pontos. Portanto no limite, a
normal à
recta 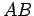 , no seu ponto
característico , no seu ponto
característico 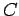 , passa pelo centro instantâneo de
rotação , passa pelo centro instantâneo de
rotação  . .
Em particular, suponhamos que uma linha (recta ou uma outra curva)
do plano móvel está condicionada a passar sempre por um
certo
ponto fixo de  (que é pois a envolvente das
sucessivas
posições dessa linha). Então, para uma
posição instantânea
de (que é pois a envolvente das
sucessivas
posições dessa linha). Então, para uma
posição instantânea
de  , a normal a essa linha, elevada a
partir desse ponto fixo, passa pelo centro instantâneo de
rotação. , a normal a essa linha, elevada a
partir desse ponto fixo, passa pelo centro instantâneo de
rotação.
Como veremos nos vários exemplos que analisaremos em breve,
estes
princípios permitem construir geomètricamente:
- o
centro instantâneo de rotação;
- as normais às trajectórias, em
 , dos pontos de , dos pontos de
 ; e ainda, ; e ainda,
- os pontos característicos em que as (sucessivas
posições das) linhas
transportadas por
 tocam as suas envolventes. tocam as suas envolventes.
Nesses exemplos, o movimento
 será definido:
será definido:
- pelas trajectórias de dois pontos de

- pela trajectória de um ponto e pela envolvente de
uma linha (que pode reduzir-se a um ponto)
- pelas envolventes de duas linhas, que compreende o caso em
que essas envolventes se reduzem a pontos
- por um ponto pelo qual uma linha de
 deve passar e pela
trajectória
de um ponto deve passar e pela
trajectória
de um ponto
- por um ponto pelo qual uma linha de
 deve passar e pela
envolvente de uma linha de deve passar e pela
envolvente de uma linha de  . .
Veremos de seguida
várias aplicações
geométricas dos princípios atrás enunciados,
designados conjuntamente pelo chamado "método
das normais".
|
|
 traçamos a
perpendicular a este segmento, e, anàlogamente, através
do
ponto médio do segmento
traçamos a
perpendicular a este segmento, e, anàlogamente, através
do
ponto médio do segmento 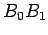 a respectiva perpendicular.
Seja
a respectiva perpendicular.
Seja 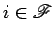 o ponto de
encontro destas duas perpendiculares.
Temos então que (porquê?):
o ponto de
encontro destas duas perpendiculares.
Temos então que (porquê?):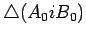 e
e
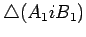 são pois
iguais e daí que:
são pois
iguais e daí que:
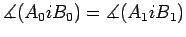
 e
e  , a que chamamos
, a que chamamos 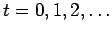 a placa
a placa
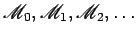 .
.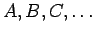 e minúsculas
e minúsculas
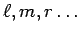 ,
respectivamente. No movimento de
,
respectivamente. No movimento de 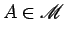 ocupará
sucessivamente as posições
ocupará
sucessivamente as posições
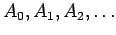 em
em
 de
de 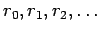 em
em
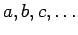 e por letras gregas
e por letras gregas
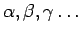 ,
respectivamente. O movimento de
,
respectivamente. O movimento de  .
. 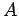 , uma recta
, uma recta 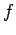 . O plano
. O plano

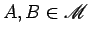 que, para duas
posições sucessivas arbitrárias de
que, para duas
posições sucessivas arbitrárias de
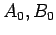 e
e 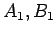 , em
, em
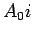
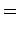
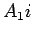
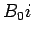
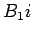


 , o ponto
, o ponto  será
transformado em
será
transformado em 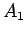 e simultâneamente,
e simultâneamente, 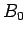 em
em  . Como a
posição de
. Como a
posição de 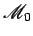 para
a
posição
para
a
posição 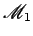 pode ser obtido por
uma rotação em torno de um
certo ponto fixo
pode ser obtido por
uma rotação em torno de um
certo ponto fixo 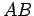 toca, numa das suas
posições, a curva envolvente das suas sucessivas
posições em
toca, numa das suas
posições, a curva envolvente das suas sucessivas
posições em
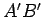 dessa
recta. Suponhamos que estas duas rectas, se intersectam num ponto
dessa
recta. Suponhamos que estas duas rectas, se intersectam num ponto 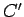 de
de 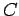 o ponto de
o ponto de 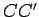 , que
passam nos respectivos pontos médios, passam todas pelo centro
de
rotação
, que
passam nos respectivos pontos médios, passam todas pelo centro
de
rotação  e
e 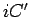 são normais
às trajectórias desses pontos. Portanto no limite, a
normal à
recta
são normais
às trajectórias desses pontos. Portanto no limite, a
normal à
recta