|
Next: A base e a
Previous: Introdução
Contents
|
|
|
|
|
|
Primeira questão
... Suponhamos que o movimento
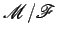 é determinado pelas trajectórias de dois pontos
de é determinado pelas trajectórias de dois pontos
de  . Determinar os pontos
característicos em que uma
curva dada, em . Determinar os pontos
característicos em que uma
curva dada, em  , toca a envolvente das suas
sucessivas
posições em , toca a envolvente das suas
sucessivas
posições em  . . |
Já vimos antes a solução - num determinado
instante, calculamos o
centro instantâneo de rotação, traçando as
normais às trajectórias dos dois pontos de
 referidos. Baixamos então, a
partir do
centro instantâneo de rotação, a normal à
posição
da curva referida, no instante considerado. O pé desta
perpendicular é o ponto característico procurado. referidos. Baixamos então, a
partir do
centro instantâneo de rotação, a normal à
posição
da curva referida, no instante considerado. O pé desta
perpendicular é o ponto característico procurado.
No applet seguinte, um segmento  , rigidamente ligado a , rigidamente ligado a  ,
move-se de tal forma que as suas extremidades percorrem duas
curvas fixas (duas elipses). O centro
instantâneo de rotação ,
move-se de tal forma que as suas extremidades percorrem duas
curvas fixas (duas elipses). O centro
instantâneo de rotação 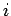 , é o ponto de
interseção das normais às elipses, nos pontos , é o ponto de
interseção das normais às elipses, nos pontos  e e 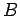 . O
ponto característico . O
ponto característico 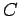 da recta da recta  ,
na posição representada, é o pé da
perpendicular baixada de ,
na posição representada, é o pé da
perpendicular baixada de 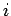 sobre essa recta. No applet, pode controlar
o ponto sobre essa recta. No applet, pode controlar
o ponto  com o rato. com o rato.
|
|
|
|
|
|
Um outro exemplo: quando
as extremidades do segmento  percorrem os lados de um
ângulo recto, a envolvente (das sucessivas
posições)
desse segmento, é um astróide; a
determinação do ponto característico percorrem os lados de um
ângulo recto, a envolvente (das sucessivas
posições)
desse segmento, é um astróide; a
determinação do ponto característico 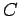 , está ilustrada no applet seguinte: , está ilustrada no applet seguinte:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As duas curvas fixas de  podem confundir-se
numa só. Por exemplo, consideremos de novo um
ângulo recto móvel cujos lados permanecem sempre tangentes
a uma
elipse (ou a uma hipérbole). A normal à curva descrita
pelo
vértice podem confundir-se
numa só. Por exemplo, consideremos de novo um
ângulo recto móvel cujos lados permanecem sempre tangentes
a uma
elipse (ou a uma hipérbole). A normal à curva descrita
pelo
vértice 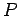 desse ângulo passa pelo ponto médio
da corda que
une os pontos de contacto desse ângulo passa pelo ponto médio
da corda que
une os pontos de contacto  e e 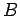 . Esta normal passa pois pelo
centro da cónica, o que prova que a trajectória descrita
por . Esta normal passa pois pelo
centro da cónica, o que prova que a trajectória descrita
por 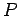 é um círculo chamado o círculo director da
cónica.
é um círculo chamado o círculo director da
cónica.
Concluindo:
"Todos
os ângulos rectos circunscritos a uma elipse (ou a uma
hipérbole) têm os seus vértices sobre um
círculo concêntrico a
essa cónica."
|
|
|
|
|
A mesma situação
ocorre para uma hipérbole:
|
|
|
Terceira questão
...
O movimento 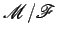
é determinado por um certo ponto
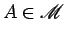 ,
que desliza sobre uma curva fixa em  , e por uma certa curva 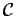 de  , que se move sempre tangencialmente a
uma curva
fixa de  .
Pretende-se determinar a normal à trajectória de um ponto
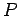 de
de  e os pontos em que as sucessivas
posições de e os pontos em que as sucessivas
posições de 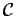 tocam a sua envolvente.
tocam a sua envolvente.
|
Solução - Num determinado instante, calculamos o centro
instantâneo de rotação 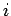 em em
 . O pé da perpendicular baixada
de . O pé da perpendicular baixada
de 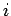 sobre a posiçãode sobre a posiçãode 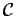 , no instante fixado é
o seu ponto característico. , no instante fixado é
o seu ponto característico.
Consideremos, por exemplo, uma elipse que se move sempre
tangencialmente a uma certa linha recta 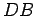 e em que um dos focos e em que um dos focos 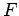 percorre uma linha recta percorre uma linha recta 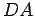 perpendicular à anterior. perpendicular à anterior.
Para obter a normal à curva descrita por um ponto, rigidamente
ligado a esta elipse, construímos o centro instantâneo de
rotação 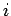 . .
Consideremos, em particular, a normal à curva descrita pelo
centro 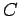 da elipse. da elipse. 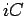 será a normal à
curva descrita por será a normal à
curva descrita por 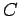 . Esta normal passa sempre pelo ponto onde
concorrem as duas rectas fixas . Esta normal passa sempre pelo ponto onde
concorrem as duas rectas fixas 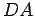 e e 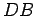 . De facto, a recta . De facto, a recta 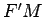 ,
onde ,
onde 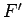 é o segundo foco,
intersecta é o segundo foco,
intersecta 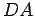 em em 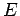 , e tem-se que , e tem-se que 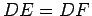 . Mas . Mas 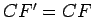 e portanto a recta e portanto a recta 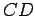 é paralela a é paralela a 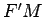 e
passa pelo ponto médio de e
passa pelo ponto médio de 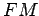 . Isto prova que esta recta . Isto prova que esta recta 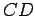 é
a diagonal do rectângulo é
a diagonal do rectângulo 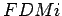 e, portanto, passa por e, portanto, passa por 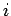 - ela
é pois a normal à curva descrita por - ela
é pois a normal à curva descrita por 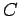 . Concluímos que . Concluímos que 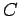 descreve um círculo centrado em
descreve um círculo centrado em 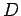 . Colocando a elipse de tal forma
que os dois focos estejam sobre a recta . Colocando a elipse de tal forma
que os dois focos estejam sobre a recta 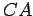 , vemos que o raio deste
círculo é igual ao semi-eixo maior. , vemos que o raio deste
círculo é igual ao semi-eixo maior.
|
|
|
Concluindo:
"Se uma elipse se move sempre
tangencialmente a um lado de um
ângulo recto de tal forma que um dos seus focos percorre o outro
lado desse ângulo, o centro da elipse descreve um círculo
cujo
centro é o vértice do ângulo e cujo raio é
igual ao semieixo
maior da elipse."
Antecipando um pouco o que se irá ver na secção 3,
estudemos o movimento inverso em que, agora, um ângulo recto se
move de tal forma que um dos lados passa sempre pelo foco de uma
elipse (ou uma hipérbole) e o outro lado se mantem sempre
tangencial a essa elipse (ou uma hipérbole).
|
|
|
|
|
|
|
|
Do foco 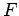 baixamos perpendiculares baixamos perpendiculares 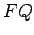 sobre as tangentes sobre as tangentes 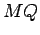 .
A normal em .
A normal em 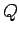 à curva
lugar geométrico dos pés destas
perpendiculares passa pelo ponto médio de à curva
lugar geométrico dos pés destas
perpendiculares passa pelo ponto médio de 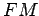 . Se prolongamos a
perpendicular . Se prolongamos a
perpendicular 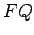 até até 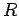 , de tal forma que , de tal forma que 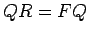 , esta normal
é paralela à recta , esta normal
é paralela à recta 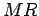 que passa no segundo foco da cónica.
Portanto a normal passa no ponto médio do segmento que une os
dois
focos, isto é, no centro da cónica. que passa no segundo foco da cónica.
Portanto a normal passa no ponto médio do segmento que une os
dois
focos, isto é, no centro da cónica.
Concluindo:
|
|
|
|
|
|
|
|
|
Next: A base e a
Previous: Introdução
Contents
Joao Nuno Tavares
2005-04-12
|
|
|
|
|
|
|
|
|
|
|
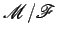 é determinado pelas trajectórias de dois pontos
de
é determinado pelas trajectórias de dois pontos
de  . Determinar os pontos
característicos em que uma
curva dada, em
. Determinar os pontos
característicos em que uma
curva dada, em  .
. , rigidamente ligado a
, rigidamente ligado a 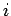 , é o ponto de
interseção das normais às elipses, nos pontos
, é o ponto de
interseção das normais às elipses, nos pontos  e
e 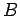 . O
ponto característico
. O
ponto característico 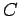 da recta
da recta 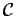 de
de 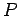 de
de 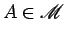 ,
que desliza sobre uma curva fixa em
,
que desliza sobre uma curva fixa em 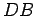 e em que um dos focos
e em que um dos focos 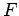 percorre uma linha recta
percorre uma linha recta 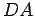 perpendicular à anterior.
perpendicular à anterior. 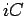 será a normal à
curva descrita por
será a normal à
curva descrita por 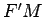 ,
onde
,
onde 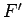 é o segundo foco,
intersecta
é o segundo foco,
intersecta 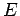 , e tem-se que
, e tem-se que 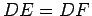 . Mas
. Mas 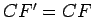 e portanto a recta
e portanto a recta 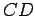 é paralela a
é paralela a 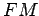 . Isto prova que esta recta
. Isto prova que esta recta 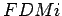 e, portanto, passa por
e, portanto, passa por 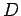 . Colocando a elipse de tal forma
que os dois focos estejam sobre a recta
. Colocando a elipse de tal forma
que os dois focos estejam sobre a recta 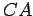 , vemos que o raio deste
círculo é igual ao semi-eixo maior.
, vemos que o raio deste
círculo é igual ao semi-eixo maior.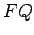 sobre as tangentes
sobre as tangentes 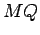 .
A normal em
.
A normal em 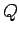 à curva
lugar geométrico dos pés destas
perpendiculares passa pelo ponto médio de
à curva
lugar geométrico dos pés destas
perpendiculares passa pelo ponto médio de 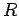 , de tal forma que
, de tal forma que 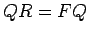 , esta normal
é paralela à recta
, esta normal
é paralela à recta 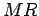 que passa no segundo foco da cónica.
Portanto a normal passa no ponto médio do segmento que une os
dois
focos, isto é, no centro da cónica.
que passa no segundo foco da cónica.
Portanto a normal passa no ponto médio do segmento que une os
dois
focos, isto é, no centro da cónica.