Exemplo 1. Um
segmento move-se de tal forma que as suas extremidades estão
sempre sobre os lados de um ângulo.
Elipsógrafo.
Teorema de de La Hire.
No
plano  fixamos dois pontos
fixamos dois pontos  e
e 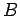 , e no plano
, e no plano  fixamos duas rectas
fixamos duas rectas 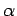 e
e 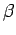 , concorrentes em
, concorrentes em
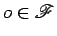 . O
plano
. O
plano  move-se sobre
move-se sobre
 de tal forma que
de tal forma que  e
e 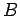 permanecem sempre em
permanecem sempre em 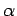 e
e 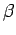 , respectivamente.
, respectivamente.
Quando
as rectas as rectas 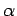 e
e 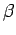 são
perpendiculares não é difícil mostrar que um ponto
são
perpendiculares não é difícil mostrar que um ponto
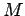 qualquer do segmento
qualquer do segmento  ,
traça uma elipse.
,
traça uma elipse.
|
|
|
Consideremos agora uma posição arbitrária do
segmento  e tracemos
o centro instantâneo de rotação
e tracemos
o centro instantâneo de rotação 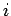 . No instante considerado,
. No instante considerado, 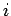 está na intersecção
das perpendiculares a
está na intersecção
das perpendiculares a 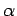 e
e 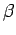 que passam,
respectivamente, nos
pontos
que passam,
respectivamente, nos
pontos  e
e 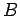 .
.
Consideremos agora o círculo circunscrito ao triângulo 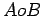 . Se supômos que este círculo
está ligado ao segmento
. Se supômos que este círculo
está ligado ao segmento  , durante o movimento ele passará
sempre pelo ponto
, durante o movimento ele passará
sempre pelo ponto  . De facto, o ângulo
. De facto, o ângulo 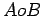 , medindo metade do
arco invariável
, medindo metade do
arco invariável  , compreendido entre os seus lados, não
pode
deixar de ser inscrito. O ponto
, compreendido entre os seus lados, não
pode
deixar de ser inscrito. O ponto 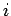 é a extremidade do diâmetro desse
círculo, e o
comprimento desse diâmetro, é igual a:
é a extremidade do diâmetro desse
círculo, e o
comprimento desse diâmetro, é igual a:
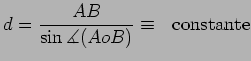
 e
e 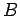 .
. 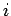 está pois sempre a uma distância
constante e igual a
está pois sempre a uma distância
constante e igual a 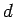 de
de  e portanto a base do movimento
e portanto a base do movimento
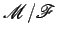 é o círculo de centro
é o círculo de centro  e raio igual a
e raio igual a 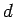 .
.
O círculo de diâmetro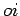 , e centro
, e centro 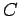 , muda de posição com
o segmento
, muda de posição com
o segmento  . Fixemos um ponto
. Fixemos um ponto 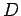 qualquer nesse círculo. O arco
qualquer nesse círculo. O arco 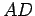 permanece sempre constante. Portanto o
ângulo
permanece sempre constante. Portanto o
ângulo 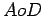 sendo
constante e tendo o seu lado
sendo
constante e tendo o seu lado 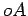 fixo, todo o ponto
fixo, todo o ponto 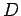 do círculo
do círculo 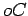 , descreve uma recta
, descreve uma recta 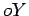 fixa em
fixa em  . Faça o teste no applet
seguinte, controlando com o rato a posição do ponto
. Faça o teste no applet
seguinte, controlando com o rato a posição do ponto  . Pode ainda redimensionar o comprimento do
segmento
. Pode ainda redimensionar o comprimento do
segmento  , a posição de
, a posição de 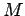 nesse segmento e ainda a
inclinação da recta
nesse segmento e ainda a
inclinação da recta 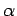 .
.
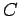 que passa pelo ponto
que passa pelo ponto 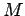 ,
as extremidades
,
as extremidades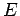 e
e 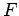 desse diâmetro descrevem,
durante o
movimento de
desse diâmetro descrevem,
durante o
movimento de  , as duas rectas fixas indicadas a azul. Estas
rectas
são perpendiculares e portanto (situação anterior
das recta
perpendiculares....)
, as duas rectas fixas indicadas a azul. Estas
rectas
são perpendiculares e portanto (situação anterior
das recta
perpendiculares....) 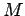 descreve uma elipse tendo como semi-eixos
descreve uma elipse tendo como semi-eixos 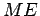 e
e 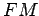 , dirigidas segundo as rectas azuis indicadas no
applet.
, dirigidas segundo as rectas azuis indicadas no
applet. O Teorema seguinte resulta do que acabamos de dizer:
| Teorema de de la Hire: No movimento descrito anteriormente, todo o ponto do círculo móvel descreve um diâmetro do círculo fixo. |
Este teorema, por sua vez, justifica o comportamento do seguinte mecanismo:
e ainda dos seguintes "mecanismos de relógio":
|
|
|
Consideremos agora o movimento inverso
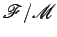 . Agora
os pontos
. Agora
os pontos  e
e 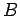 estão fixos enquanto que as rectas
estão fixos enquanto que as rectas 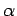 e
e 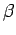 ,
formando sempre um ângulo constante, passam respectivamente por
,
formando sempre um ângulo constante, passam respectivamente por  e
e 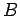 . Nos applets seguintes representamos os dois
movimentos
(as rectas
. Nos applets seguintes representamos os dois
movimentos
(as rectas 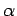 e
e 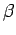 são
perpendiculares, nestes applets):
são
perpendiculares, nestes applets): |
|
|
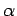 e
e 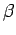 , fazem sempre um
ângulo constante
entre si, as perpendiculares
, fazem sempre um
ângulo constante
entre si, as perpendiculares 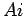 e
e 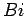 a essas rectas formam
também um ângulo constante entre si.
a essas rectas formam
também um ângulo constante entre si. 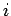 está pois sempre
sobre o arco que subentende a corda
está pois sempre
sobre o arco que subentende a corda  do círculo e portanto sobre
o círculo circunscrito ao triângulo
do círculo e portanto sobre
o círculo circunscrito ao triângulo 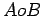 , que é por isso a
rolante do movimento.
, que é por isso a
rolante do movimento. Next: Exemplo 2. Um ângulo Previous: A base e a Contents Joao Nuno Tavares 2005-04-12