Exemplo 2. Um ângulo move-se de tal forma que os seus lados são sempre tangenciais a dois círculos dados
No plano  consideramos duas rectas
consideramos duas rectas  e
e  , que se
intersectam no
ponto
, que se
intersectam no
ponto  segundo um ângulo
constante, e, no plano
segundo um ângulo
constante, e, no plano  , dois
círculos
, dois
círculos  e
e  , de centros
, de centros  e
e  , respectivamente. No
movimento
, respectivamente. No
movimento 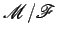 a recta
a recta
 mantem-se sempre tangente a
mantem-se sempre tangente a  e
a recta
e
a recta  sempre tangente a
sempre tangente a  , como no applet seguinte:
, como no applet seguinte:
Pelos pontos  e
e  tracemos paralelas a
tracemos paralelas a  e
e  ,
respectivamente, que se intersectam em
,
respectivamente, que se intersectam em  . Durante o movimento,
este ponto
. Durante o movimento,
este ponto  permanece sempre sobre o
círculo que passa em
permanece sempre sobre o
círculo que passa em  e
e
 , uma vez que o ângulo
, uma vez que o ângulo  é
sempre
constante. Por outro lado o ponto
é
sempre
constante. Por outro lado o ponto  está rigidamente ligado a
está rigidamente ligado a
 , já que as suas
distâncias às rectas
, já que as suas
distâncias às rectas  e
e  , de
, de
 , são constantes (e iguais aos
raios dos círculos). O segmento
, são constantes (e iguais aos
raios dos círculos). O segmento
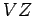 tem pois comprimento constante
e faz sempre os mesmos
ângulos com as rectas
tem pois comprimento constante
e faz sempre os mesmos
ângulos com as rectas  e
e  .
.
Resulta daqui que, durante o movimento 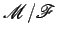 , a
recta
, a
recta 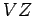 passa
sempre por um mesmo ponto
passa
sempre por um mesmo ponto  do círculo
do círculo  e portanto o
ponto
e portanto o
ponto  descreve um concóide de
círculo (ver o Apêndice), de
pólo
descreve um concóide de
círculo (ver o Apêndice), de
pólo  e módulo
e módulo
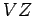 . De facto é um
limaçon de Pascal (veja o applet).
. De facto é um
limaçon de Pascal (veja o applet).
É claro que o centro instantâneo de rotação é o ponto
 de encontro das normais a
de encontro das normais a  e
e  traçadas a partir dos
pontos de tangência com os círculos
dados. A recta
traçadas a partir dos
pontos de tangência com os círculos
dados. A recta  é pois normal ao limaçon de Pascal
descrito
por
é pois normal ao limaçon de Pascal
descrito
por  e, recorrendo a uma normal a
e, recorrendo a uma normal a  , passando em
, passando em  , obtemos
uma descrição tangencial desse mesmo limaçon.
, obtemos
uma descrição tangencial desse mesmo limaçon.O movimento
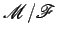 pode
também ser obtido pelo movimento do ângulo constante
pode
também ser obtido pelo movimento do ângulo constante  , que se
desloca de tal forma que os seus lados passam sempre pelos pontos fixos
, que se
desloca de tal forma que os seus lados passam sempre pelos pontos fixos
 e
e  . Este movimento é, por sua vez, o inverso
do movimento em que o segmento de recta constante que une
. Este movimento é, por sua vez, o inverso
do movimento em que o segmento de recta constante que une  a
a  , se desloca de tal forma que as suas
extremidades percorrem os lados do ângulo
, se desloca de tal forma que as suas
extremidades percorrem os lados do ângulo  , e que
foi estudado no exemplo anterior. Portanto a base e a rolante do
movimento
, e que
foi estudado no exemplo anterior. Portanto a base e a rolante do
movimento 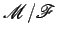 são, respectivamente, o círculo
são, respectivamente, o círculo  e o círculo
centrado em
e o círculo
centrado em  e de raio igual à
distância de
e de raio igual à
distância de  a
a 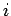 .
.Nos applets seguintes mostram-se os dois movimentos
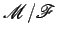 e o seu
inverso .
e o seu
inverso .|
|
|
Next: Exemplo 3. Três barras Previous: Exemplo 1. Um segmento Contents Joao Nuno Tavares 2005-04-12