Fixemos uma curva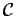 
(a base) e um ponto 
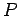(o pólo). Na base 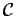, consideremos um ponto variável 
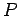. Na recta que une o pólo ao ponto , considerem-se os dois pontos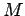 
, que estão a uma distância fixa 
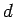de 
.
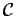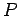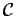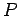(a base) e um ponto (o pólo). Na base , consideremos um ponto variável . Na recta que une o pólo ao ponto , considerem-se os dois pontos 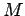, que estão a uma distância fixa 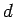de . O lugar geométrico destes pontos
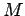, quando varia na base, diz-se o concóide da curva 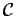relativamente ao pólo 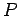.Quando
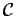é uma recta o conchóide chama-se o concóide de Nicomedes.
O limaçon de Pascal é o concóide de um círculo, relativamente a um pólo situado sobre esse mesmo círculo:
Back to: Exemplo 2 Contents Joao Nuno Tavares 2005-04-12