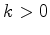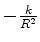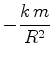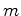Leis de Kepler e

Lei da atracção universal de Newton
                                                                                                                                                                                                                       
   Tycho Brahe
    (1546-1601)      


Johann Kepler (1571-1630)
   











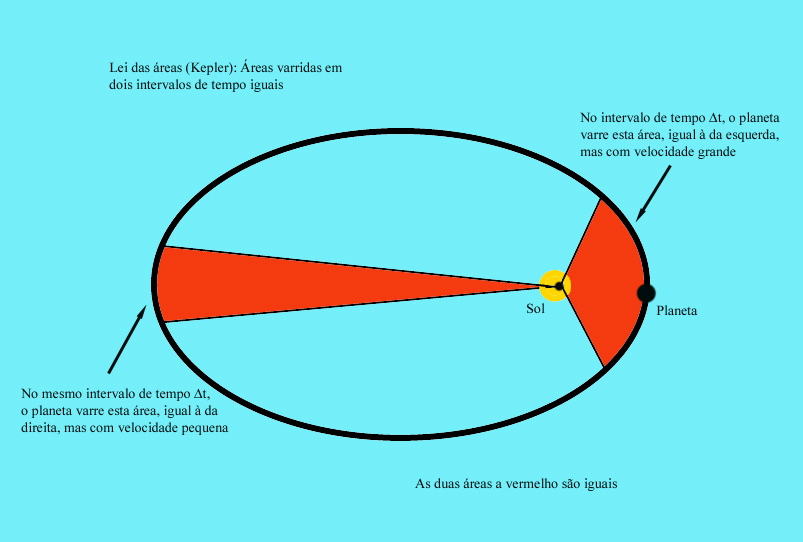
No princípio do século XVII, Johann Kepler (1571-1630), a partir de uma grande quantidade de observações astronómicas efectuadas por Tycho Brahe (1546-1601), nos últimos 20 anos da sua vida, formulou as seguintes três leis para o movimento dos planetas em torno do Sol:

                  
   Primeira Lei de Kepler
  [Lei das elipses]  

 ``Cada planeta move-se sobre uma elipse com o sol num dos focos" .


                  
Segunda Lei de Kepler
 [Lei das áreas] 

``O vector de posição de cada planeta, relativamente ao sol, varre áreas iguais em tempos iguais" .


 
Terceira Lei de Kepler
[Lei dos períodos] 

``O quadrado do período (i.e., o tempo necessário para completar uma órbita) é proporcional ao cubo do eixo maior da elipse, sendo a constante de proporcionalidade a mesma para todos os planetas" .





Por favor habilite Java para uma construção interativa (com Cinderella).




Isaac Newton (1642-1727)


Cerca de 50 anos mais tarde, Isaac Newton (1642-1727) utilizou a sua própria lei:

``Força = massa $ \times$ aceleração"

para deduzir, a partir das leis de Kepler, a natureza básica da força que mantém cada planeta na respectiva órbita.


Lei da atracção universal de Newton
  

 As duas primeiras Leis de Kepler implicam que a força exercida sobre cada planeta, é uma força central, cujo centro é o Sol.

Além disso, existe uma constante $ k>0$ , a mesma para todo o planeta, tal que a aceleração radial é igual a $ -\frac{k}{R^2}$. Portanto, a intensidade da força de atracção exercida sobre cada planeta, é igual a:

$\displaystyle -\frac{k \, m}{R^2}$ (1)

isto é, é proporcional à massa $ m$ desse planeta, e proporcional ao inverso do quadrado da sua distância ao Sol.
 




Recìprocamente, é possível deduzir as leis de Kepler a partir da lei de atracção universal de Newton e da lei de Newton.




Página seguinte: Os problemas directo e inverso
Regresso ao Índice