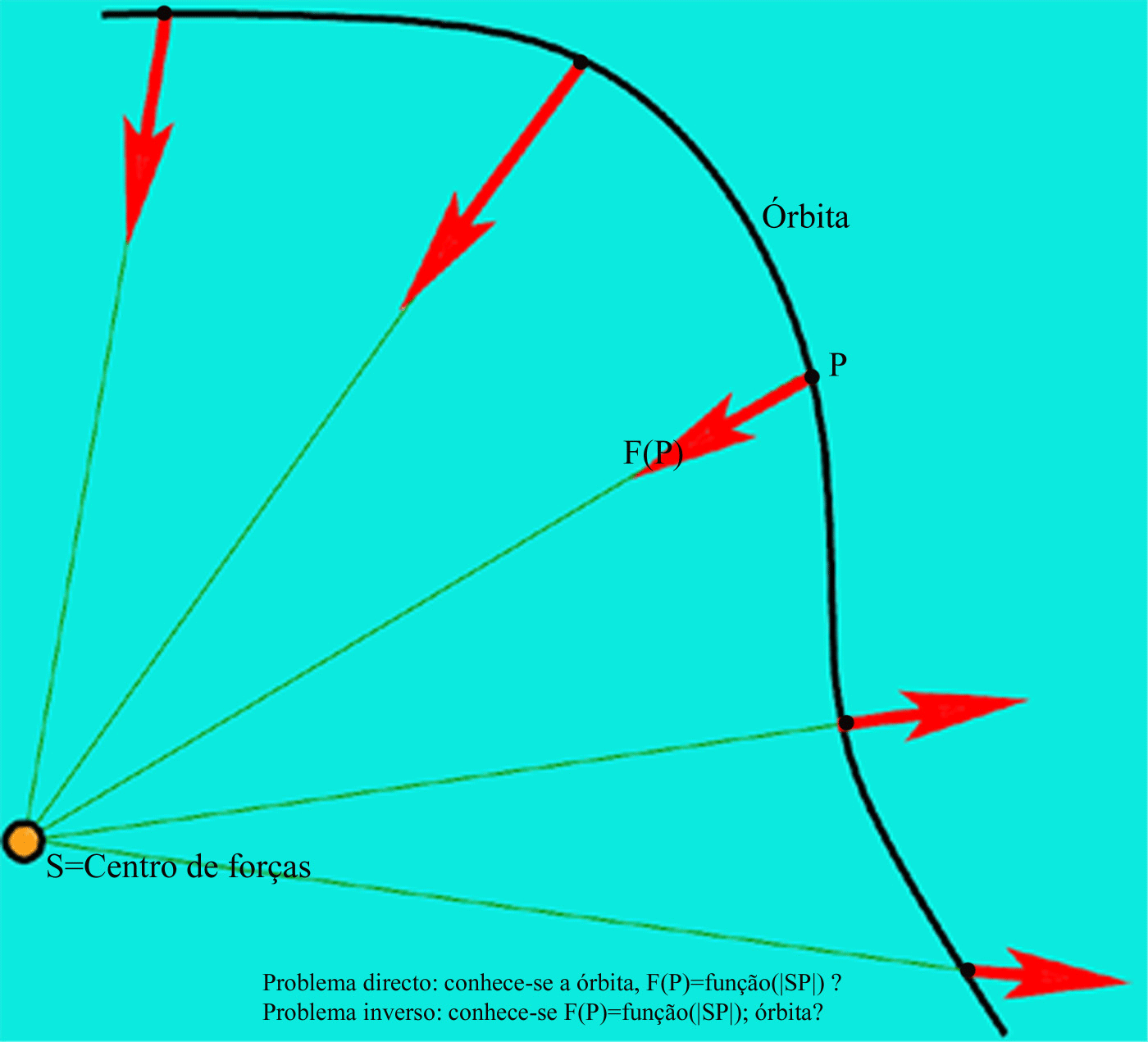
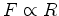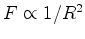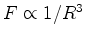Os problemas directo e inverso


Problema directo


Dada uma trajectória de um planeta $ P$ e um centro de forças $ S$ fixo, determinar a forma como depende a força da distância entre $ P$ e $ S$ :
$\displaystyle F(P) \stackrel{\boldmath {?}}{=} \hbox{fun{\c c\~ao}\, de} \ \ \vert PS\vert$ (2)


Problema inverso




     Conhecida a força central determinar a trajectória do  planeta.










Em 1687 Newton usou um método de aproximação poligonal para demonstrar a lei das áreas de Kepler, válida para qualquer força central. Usando este resultado e novamente argumentos de aproximação, Newton criou um método geral para resolver o problema directo, isto é, um método geométrico que permite determinar a natureza da força, responsável por um dado movimento orbital em torno de um centro de forças fixo.

Os exemplos ilustrativos deste método geral, incluídos na sua grande obra ``Principia Mathematica", foram os seguintes:


Órbita Centro de forças Força
Círculo Centro do círculo Constante
Círculo Um ponto qualquer
no círculo
 $ F \propto 1/R^5$
Elipse Centro da elipse $ F \propto R$
Elipse Um foco da elipse $ F \propto 1/R^2$
Espiral Pólo da espiral $ F \propto 1/R^3$


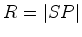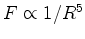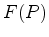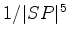onde pusemos $ R=\vert SP\vert$ e, por exemplo, $ F \propto 1/R^5$ significa ``$ F(P)$ é proporcional a $ 1/\vert SP\vert^5$ ".
 
O método de Newton e estes exemplos serão tratados em breve num trabalho a incluir nesta área de divulgação do CMUP.




Página seguinte: Como Newton e Feynman provam a lei das áreas
Página anterior: Leis de Kepler e Lei da atracção universal de Newton
Regresso ao Índice