1. De quantas maneiras distintas podemos pintar os vértices de um triângulo equilátero, |
||
|
Para responder
podemos fazer contagem directa - cada vértice pode ser pintado
de duas maneiras diferentes (branco ou preto). Como temos 3
vértices temos 2x2x2=8 maneiras de pintar os 3 vértices.
Portanto existem as 8 colorações seguintes:
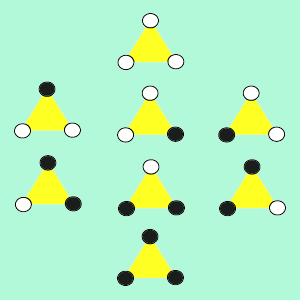 |
||
|
No entanto, se
identificarmos duas colorações que diferem entre si por
rotação do triângulo de 120º ou
de 240º, em torno do
seu centro, então as 3 colorações da segunda linha
devem ser consideradas a mesma. Analogamente as 3
colorações da terceira linha devem ser consideradas a
mesma. Existem pois 4 "padrões" distintos - um com 3
vértices brancos, um com 1 preto e 2 brancos, outro com 2 pretos
e 1 branco e, finalmente, um com 3 pretos.
|
||
|
|
||
2. De quantas
maneiras distintas podemos pintar os vértices de um
quadrado,
|
||
Para
responder podemos fazer contagem directa - cada vértice pode ser
pintado de duas maneiras diferentes (branco ou preto). Como temos 4
vértices temos 2x2x2x2=16 maneiras de pintar os 4
vértices. Portanto
existem as 16 colorações seguintes: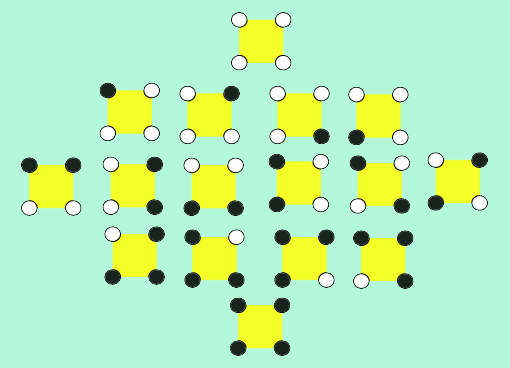 |
||
| No entanto, se
identificarmos duas colorações que diferem entre si por
rotação do quadrado de 90º,
180º ou de 270º, em torno do
seu centro, então existem
apenas 6 "padrões" distintos - quais? |
||
|
|
||
| Página
seguinte Índice |