| Introdução |
|
|
|
Existem várias aplicações muito importantes do
teorema de Polya.
Por exemplo:
- contagem de grafos
- contagem de compostos químicos (isómeros)
- contagem de objectos musicais (acordes, padrões
rítmicos, séries tonais, etc)
Estas aplicações
serão tratadas brevemente nesta Área
de
Divulgação Matemática do CMUP.
Para essas
aplicações
é conveniente reformular o teorema de Polya
usando uma linguagem mais abrangente e figurativa.
|
|
Conteúdo
de uma figura
|
|
|
|
Como na secção
anterior,
seja:
-
 um
conjunto
finito de objectos (caixas, posições, etc). um
conjunto
finito de objectos (caixas, posições, etc).
-
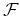 um
conjunto
finito de ``figuras", "cores", etc. um
conjunto
finito de ``figuras", "cores", etc.
A cada figura 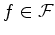 é
atribuído um
conteúdo
que é um inteiro não negativo: é
atribuído um
conteúdo
que é um inteiro não negativo:
|
|
Série
enumerativa
de
figuras |
|
|
|
- A série
enumerativa
de
figuras é, por definição, a
série:
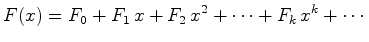 |
(30) |
onde:
|
|
Configurações
Padrões
|
|
|
|
diz-se uma configuração (ou coloração, como antes) .
Uma configuração é pois uma maneira de pôr
uma figura em cada
caixa, permitindo que a mesma figura seja posta em duas ou mais
caixas (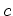 não precisa de ser
injectiva). não precisa de ser
injectiva).
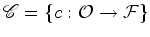 é
o
conjunto das configurações em
é
o
conjunto das configurações em  .
.
- Suponhamos agora que temos um grupo
que
actua (à esquerda) no
conjunto
 dos
objectos: dos
objectos:
Esta acção induz uma
acção (à
esquerda) no conjunto
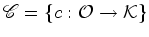 das
configurações de das
configurações de  , definida por:
, definida por:
onde:
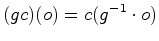 |
(32) |
- Como antes, duas
configurações
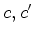 dizem-se
equivalentes se e
só
se pertencem à mesma órbita da acção de dizem-se
equivalentes se e
só
se pertencem à mesma órbita da acção de 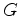 em em 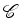 , isto é, sse
existe
, isto é, sse
existe 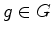 tal que tal que 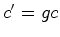 .
.
- Uma classe de
equivalência
(=órbita) diz-se um padrão. O
padrão da configuração
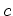 nota-se, como antes, por
nota-se, como antes, por ![$ [c]$](index1_files/img219.gif) .
.
|
|
O
problema
|
|
|
|
O problema consiste
em contar quantos
padrões ![$ [c]$](index1_files/img219.gif) existem
e exibir um inventário dos diversos
padrões.
existem
e exibir um inventário dos diversos
padrões.
|
|
|
Conteúdo
de uma configuração
|
|
|
|
- O conteúdo
 de uma
configuração de uma
configuração 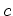 é
a soma
dos conteúdos das figuras utilizadas por
essa configuração: é
a soma
dos conteúdos das figuras utilizadas por
essa configuração:
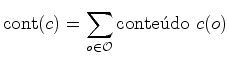 |
(33) |
Por exemplo,
no caso dos colares de pérolas brancas e pretas
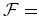 {Branca,
Preta}, com conteúdo(Branca)=0
e
conteúdo(Preta)=1, a série enumerativa de figuras
reduz-se a: {Branca,
Preta}, com conteúdo(Branca)=0
e
conteúdo(Preta)=1, a série enumerativa de figuras
reduz-se a:
O conteúdo
 de uma
configuração
(=coloração) de uma
configuração
(=coloração) 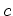 é
pois igual ao seu número de bolas pretas.
é
pois igual ao seu número de bolas pretas.
- Se atribuírmos o peso
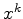 a
cada
figura a
cada
figura 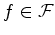 de
conteúdo
de
conteúdo  : :
vemos que:
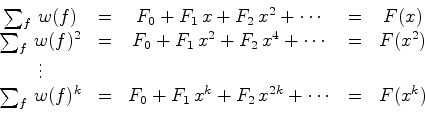 |
(34) |
Por outro lado, o peso total
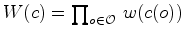 de uma
configuração
de uma
configuração
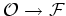 (veja (21)),
é dado por:
(veja (21)),
é dado por:
Como antes, o peso 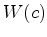 é o
mesmo para todos os elementos da órbita
de
é o
mesmo para todos os elementos da órbita
de 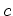 :
: 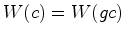 . Podemos pois falar do peso de um padrão
(=órbita):
. Podemos pois falar do peso de um padrão
(=órbita): ![$ W([c])=W(c)$](img304.gif) . Por (35)
tem-se que:
. Por (35)
tem-se que:
![$\displaystyle W([c])=x^{ \hbox{\small cont $c $} }$](img305.gif) |
(36) |
|
|
| Série
enumerativa de
padrões |
|
|
|
A série enumerativa
de
padrões conta o número total de
padrões. Como a cada padrão está atribuído
um peso, de acordo com
(36),
essa série é:
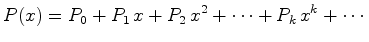 |
(37) |
onde
|
|
| De
novo o inventário de
padrões |
|
|
|
Recorde que o inventário de
padrões 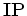 foi definido por
foi definido por
![$ \hbox{\bf IP}=\sum_{[c]\in{\mathscr{C}}/G}\, W([c])$](img314.gif) .
Portanto: .
Portanto:
Por outro
lado, o teorema de Polya diz que:
e, usando as
relações
(34)
vemos que:
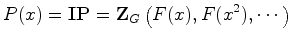 |
(39) |
Obtemos assim a seguinte
reformulação do teorema de
Polya:
|
|
Teorema
de
Polya
(segunda versão)
|
|
|
|
|
|
Aplicação
|
|
|
|
Quantos padrões
de colares de 8 pérolas
brancas e
pretas
existem??
Como vimos o índice de ciclos de 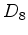 é:
é:
Substituindo 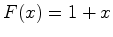 obtemos a
série enumerativa de padrões:
obtemos a
série enumerativa de padrões:
que se reduz a:
Logo existem 30
colares. Destes existem, por exemplo, 8
com 4
brancas e 4
pretas, etc....
|
|
|
|
|
REFERÊNCIAS
|
|
|
|
- V. Krishnamurthy,
"Combinatorics, theory and applications", John Wiley & Sons, 1986
- de Brujn, N.G. "Polya's
theory of counting" in Applied Combinatorial Mathematics, eds.
Beckenbach, pag. 144-184, Wiley, 1964
- Tucker, A. "Applied
Combinatorics", Wiley, 1980.
|
|
|
|
|
|
Página
anterior
Índice |
|

 não precisa de ser
injectiva).
não precisa de ser
injectiva).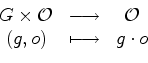
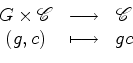
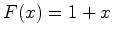
 de uma
configuração
(=coloração)
de uma
configuração
(=coloração) 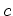 é
pois igual ao seu número de bolas pretas.
é
pois igual ao seu número de bolas pretas.
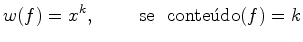
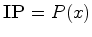
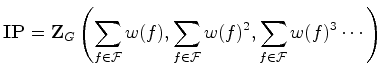

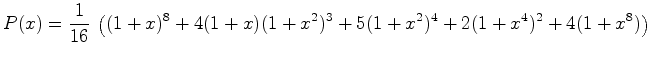
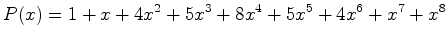

 um
conjunto
finito de objectos (caixas, posições, etc).
um
conjunto
finito de objectos (caixas, posições, etc).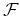 um
conjunto
finito de ``figuras", "cores", etc.
um
conjunto
finito de ``figuras", "cores", etc.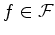
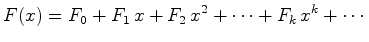
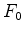
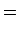
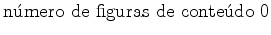
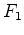
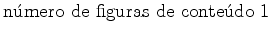
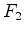
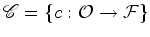
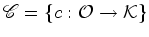 das
configurações de
das
configurações de 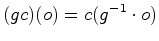
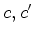
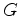
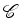
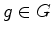
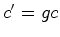
![$ [c]$](index1_files/img219.gif)
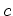 é
a soma
dos conteúdos das figuras utilizadas por
essa configuração:
é
a soma
dos conteúdos das figuras utilizadas por
essa configuração: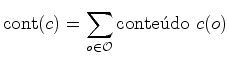
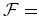 {Branca,
Preta}, com conteúdo(Branca)=0
e
conteúdo(Preta)=1, a série enumerativa de figuras
reduz-se a:
{Branca,
Preta}, com conteúdo(Branca)=0
e
conteúdo(Preta)=1, a série enumerativa de figuras
reduz-se a: 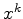 a
cada
figura
a
cada
figura 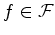 de
conteúdo
de
conteúdo  :
: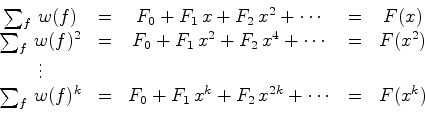
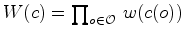 de uma
configuração
de uma
configuração
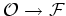 (veja (
(veja (



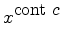
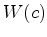 é o
mesmo para todos os elementos da órbita
de
é o
mesmo para todos os elementos da órbita
de 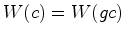 . Podemos pois falar do peso de um padrão
(=órbita):
. Podemos pois falar do peso de um padrão
(=órbita): ![$ W([c])=W(c)$](img304.gif) . Por (
. Por (![$\displaystyle W([c])=x^{ \hbox{\small cont $c $} }$](img305.gif)
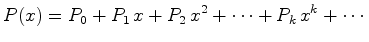
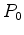
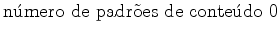
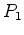
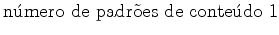
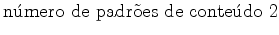

 foi definido por
foi definido por
![$ \hbox{\bf IP}=\sum_{[c]\in{\mathscr{C}}/G}\, W([c])$](img314.gif) .
Portanto:
.
Portanto: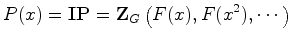
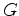 actua
num conjunto de configurações
actua
num conjunto de configurações
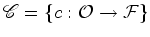 e seja
e seja 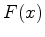 a série enumerativa de figuras.
a série enumerativa de figuras. 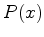 , obtida
substituindo
, obtida
substituindo  em
cada
em
cada 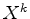 no
índice de ciclos de
no
índice de ciclos de 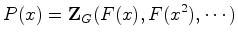
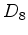 é:
é: 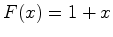 obtemos a
série enumerativa de padrões:
obtemos a
série enumerativa de padrões: