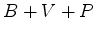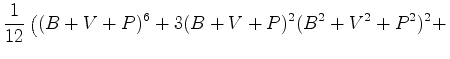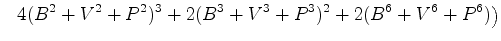| Colorações |
|
|
|
Para responder a questões deste tipo, convém generalizar
as situações já descritas, colocando-as num quadro
mais geral. Para isso analisemos o que há de essencial nos
exemplos anteriores.
Essencialmente o que temos é:
-
 um
conjunto
finito de objectos. um
conjunto
finito de objectos.
-
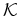 um
conjunto
finito de ``cores". um
conjunto
finito de ``cores".
Uma aplicação:
diz-se uma coloração dos
objectos em  , usando
as cores de , usando
as cores de 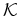 . .
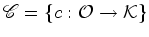 diz-se o conjunto das
colorações de diz-se o conjunto das
colorações de
 . .
Na questão que dá o
título a esta secção, temos que:
-
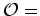 {vértices
de um polígono regular
de {vértices
de um polígono regular
de 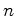 vértices} (os pontos
onde colocamos as pérolas do colar) e
vértices} (os pontos
onde colocamos as pérolas do colar) e
-
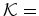 {Branco,
Vermelho, Preto} é o conjunto das cores das
pérolas. {Branco,
Vermelho, Preto} é o conjunto das cores das
pérolas.
|
|
Padrões
|
|
|
|
- Suponhamos agora que temos um grupo que
actua (à esquerda) no
conjunto
 dos objectos: dos objectos:
Esta acção induz uma
acção (à
esquerda) no conjunto
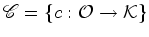 das
colorações de das
colorações de  , definida por:
, definida por:
Isto significa que cada elemento 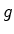 do
grupo transforma uma dada coloração do
grupo transforma uma dada coloração 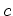 numa outra coloração
numa outra coloração 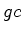 . Esta última define-se por:
. Esta última define-se por:
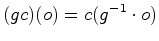 |
(20) |
isto é, a côr que 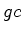 atribui ao objecto
atribui ao objecto 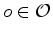 é
a côr que tem o objecto é
a côr que tem o objecto 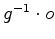 (o
objecto (o
objecto 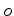 antes de ``rodar").
antes de ``rodar").
Como antes, duas colorações 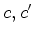 dizem-se equivalentes
quando pertencem à mesma órbita da acção de dizem-se equivalentes
quando pertencem à mesma órbita da acção de
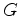 em em
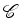 , isto é,
quando existe
, isto é,
quando existe 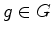 tal que
tal que 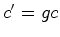 .
.
Uma classe de equivalência (=
órbita) diz-se um padrão. O
padrão da coloração 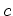 nota-se por
nota-se por ![$ [c]$](index1_files/img219.gif) .
.
|
|
O problema
|
|
|
|
O problema consiste em contar
quantos
padrões existem e
ainda exibir um inventário dos diversos padrões.
|
|
|
Pesos
|
|
|
|
- Para isso, vamos atribuir um peso
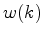 a cada côr em a cada côr em 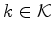 .
Por exemplo, quando .
Por exemplo, quando 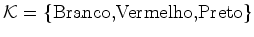 é o
conjunto das cores das
pérolas, atribuímos os pesos:
é o
conjunto das cores das
pérolas, atribuímos os pesos:
Os pesos são
variáveis formais independentes que geram
uma álgebra
(podem ser adicionados e multiplicados formalmente). Um deles pode
ser escolhido para desempenhar o papel de uma unidade 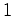 .
.
- O peso
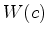 de uma coloração
de uma coloração 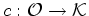 é, por
definição, igual ao produto dos pesos das cores usadas em
é, por
definição, igual ao produto dos pesos das cores usadas em
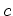 : :
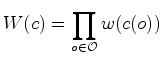 |
(21) |
Note que o peso de duas
colorações equivalentes é
o mesmo.
Portanto faz sentido falar no peso
de cada padrão ![$ [c]\in {\mathscr{C}}/G$](index1_files/img227.gif) . Basta pôr:
. Basta pôr:
|
|
O
inventário de padrões
|
|
|
|
Vamos agora construir uma série
enumerativa de potências IP, chamada o inventário de
padrões, usando os pesos de cada padrão.
Define-se por:
![$\displaystyle \hbox{\bf IP}=\sum_{[c]\in{\mathscr{C}}/G}\, W([c])$](index1_files/img229.gif) |
(22) |
Como veremos, no caso dos colares,
o coeficiente do monómio 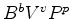 do
inventário
de padrões do
inventário
de padrões  , dá o número de
colares que têm exactamente b
pérolas brancas, v pérolas
vermelhas e p pérolas pretas.
, dá o número de
colares que têm exactamente b
pérolas brancas, v pérolas
vermelhas e p pérolas pretas.
|
|
Teorema
de Polya
|
|
|
|
|
Teorema de Polya
O
inventário de padrões é
dado em termos do índice de ciclos de 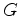 , através da fórmula:
, através da fórmula:
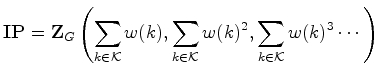 |
(23) |
|
|
|
Como
aplicar o
teorema de Polya
|
|
|
|
Apliquemos a fórmula de Polya (23)
à situação dos colares.
- Quantos
padrões de colares existem com 6 pérolas b das quais
são brancas, e p
são pretas (b+p=6) ?
Aqui 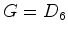 .
. 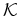 e os
pesos são os que já se
indicaram antes. O
índice de ciclos de e os
pesos são os que já se
indicaram antes. O
índice de ciclos de 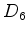 é, como
vimos antes:
é, como
vimos antes:
Como:
o inventário de
padrões
é:
Desenvolvendo,
o coeficiente de 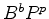 dá o número de colares com 6
pérolas, b das quais são brancas,
e p são pretas (b+p=6).
dá o número de colares com 6
pérolas, b das quais são brancas,
e p são pretas (b+p=6).
- Quantos colares
existem com 6
pérolas, b das
quais são brancas, v são vermelhas e p são pretas (b+v+p=6)?
Aqui 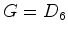 e
e 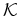 e os
pesos são os que já se
indicaram antes. O
índice de ciclos de e os
pesos são os que já se
indicaram antes. O
índice de ciclos de 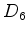 é, como
vimos antes:
é, como
vimos antes:
Como:
o inventário de
padrões
é:
Desenvolvendo, o coeficiente de 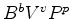 dá o
número de colares com 6
pérolas, b das quais são brancas, v são vermelhas
e p são pretas (b+v+p=6). dá o
número de colares com 6
pérolas, b das quais são brancas, v são vermelhas
e p são pretas (b+v+p=6).
|
|
|
|
|
|
Demonstração
do Teorema de Polya
|
|
|
|
|
|
Página
seguinte
Página
anterior
Índice |
|
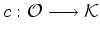
 , usando
as cores de
, usando
as cores de 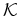 .
.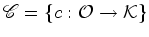 diz-se o conjunto das
colorações de
diz-se o conjunto das
colorações de
 .
. 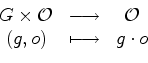
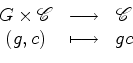
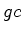 atribui ao objecto
atribui ao objecto 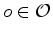 é
a côr que tem o objecto
é
a côr que tem o objecto 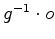 (o
objecto
(o
objecto 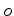 antes de ``rodar").
antes de ``rodar").
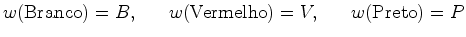
![$\displaystyle W([c])=W(c)$](index1_files/img228.gif)
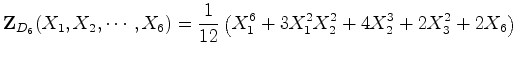
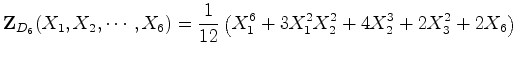
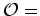 {vértices
de um polígono regular
de
{vértices
de um polígono regular
de 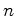 vértices} (os pontos
onde colocamos as pérolas do colar) e
vértices} (os pontos
onde colocamos as pérolas do colar) e 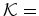 {Branco,
Vermelho, Preto} é o conjunto das cores das
pérolas.
{Branco,
Vermelho, Preto} é o conjunto das cores das
pérolas.  dos objectos:
dos objectos: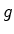 do
grupo transforma uma dada coloração
do
grupo transforma uma dada coloração 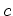 numa outra coloração
numa outra coloração 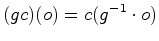
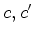
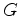 em
em
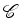 , isto é,
quando existe
, isto é,
quando existe 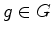 tal que
tal que 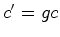 .
. 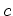 nota-se por
nota-se por ![$ [c]$](index1_files/img219.gif) .
. 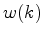
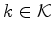 .
Por exemplo, quando
.
Por exemplo, quando 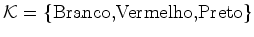 é o
conjunto das cores das
pérolas, atribuímos os pesos:
é o
conjunto das cores das
pérolas, atribuímos os pesos: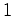 .
. 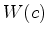
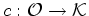
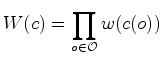
![$ [c]\in {\mathscr{C}}/G$](index1_files/img227.gif) . Basta pôr:
. Basta pôr:![$\displaystyle \hbox{\bf IP}=\sum_{[c]\in{\mathscr{C}}/G}\, W([c])$](index1_files/img229.gif)
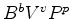 do
inventário
de padrões
do
inventário
de padrões  , dá o número de
colares que têm exactamente b
pérolas brancas, v pérolas
vermelhas e p pérolas pretas.
, dá o número de
colares que têm exactamente b
pérolas brancas, v pérolas
vermelhas e p pérolas pretas. 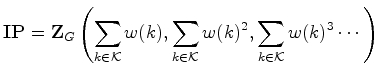
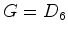 .
. 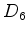 é, como
vimos antes:
é, como
vimos antes: 
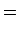
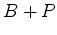
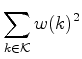

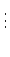
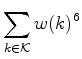
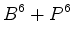
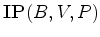
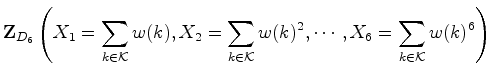
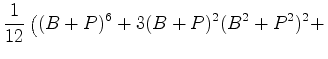
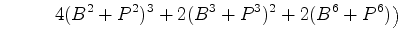
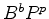 dá o número de colares com 6
pérolas, b das quais são brancas,
e p são pretas (b+p=6).
dá o número de colares com 6
pérolas, b das quais são brancas,
e p são pretas (b+p=6).