Teorema de Pascal
| Hexagrama |
|||
|
|||
| Teorema de Pascal | |||
|
O teorema fundamental sobre esta configuração foi descoberto por Blaise Pascal (1623-1662), com a idade de 16 anos, e foi publicado num artigo intitulado ``Essai sur les coniques". Diz o seguinte:
A recta que contem os pontos
colineares, referidos no teorema,
chama-se a recta de Pascal.
|
|||
|
Nos applets
seguintes, consideramos uma elipse e uma hipérbole,
respectivamente, e um hexagrama inscrito em cada uma. Os pontos de
intersecção dos pares de lados opostos foram notados por: 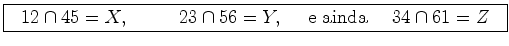 A recta de Pascal, sobre a qual
estão alinhados os pontos |
|||
 , consiste de:
, consiste de:
 - os vértices
-
situados não importa onde sobre a cónica, e
- os vértices
-
situados não importa onde sobre a cónica, e  - os lados
do
hexagrama.
- os lados
do
hexagrama. 
 e
e 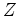 , é a recta cor de laranja. Nos applets pode, com o rato,
mudar a forma da cónica, actuando sobre os pontos pretos, e pode
mudar também a posição dos pontos amarelos do
hexagrama para
obter várias configurações.
, é a recta cor de laranja. Nos applets pode, com o rato,
mudar a forma da cónica, actuando sobre os pontos pretos, e pode
mudar também a posição dos pontos amarelos do
hexagrama para
obter várias configurações.