| Configurações
especiais |
|
|
|
Fazendo coincidir
alguns dos vértices do hexagrama
de Pascal, obtemos certas configurações especiais, que
conduzem a
alguns corolários do Teorema de Pascal que têm interesse
especial.
Vejamos alguns exemplos.
|
|
Corolário
1
|
|
|
|
- Faça, no applet anterior, coincidir,
por exemplo, os
vértices
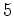 e e  , movendo o vértice
, movendo o vértice  até que ele se
sobreponha ao vértice até que ele se
sobreponha ao vértice 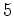 . .
- O lado
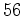 convergirá então para a recta
tangente à cónica
no ponto convergirá então para a recta
tangente à cónica
no ponto 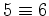 , e o hexagrama transforma-se num pentagrama
inscrito na cónica:
, e o hexagrama transforma-se num pentagrama
inscrito na cónica:
Obtemos assim o seguinte:
Corolário
3.1 ...
Num pentagrama inscrito numa
cónica, os pontos
de intersecção de dois pares de lados não
adjacentes e o ponto
de intersecção do quinto lado com a tangente que passa no
vértice oposto, estão alinhados.
|
|
|
| Corolário
2 |
|
|
|
- Faça agora coincidir, por exemplo,
os
vértices
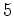 e e  e também os vértices e também os vértices  e e  .
.
- O lado
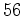 convergirá para a recta tangente no ponto convergirá para a recta tangente no ponto
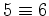 , o lado
, o lado  convergirá para a recta
tangente no ponto convergirá para a recta
tangente no ponto
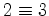 , e o hexagrama
transforma-se no tetragrama , e o hexagrama
transforma-se no tetragrama 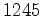 .
.
- Os lados opostos
 e e 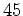 e, e, 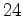 e e 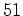 , bem como as tangentes
nos vértices opostos
, bem como as tangentes
nos vértices opostos  e e 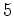 intersectam-se em pontos alinhados. intersectam-se em pontos alinhados.
- Mas como poderíamos também
ter escolhido os outros dois
vértices opostos, os pontos de intersecção destes
vértices
estão ainda sobre a recta de Pascal.
Obtemos assim o seguinte:
Corolário
3.2 ...
Num tetragrama inscrito numa cónica, os
pares de lados opostos e as tangentes nos pares de
vértices opostos, intersectam-se em pontos alinhados.
|
|
|
| Corolário
3 |
|
|
|
- Finalmente faça coincidir os
vértices
 e e  , os vértices
, os vértices  e e 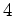 e ainda vértices e ainda vértices 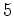 e e  . O hexagrama transforma-se num trilátero
inscrito na cónica e obtemos assim o seguinte:
. O hexagrama transforma-se num trilátero
inscrito na cónica e obtemos assim o seguinte:
Corolário
3.3 ...
Num trilátero inscrito numa
cónica,
os pontos de intersecção de cada um dos lados com a
tangente no vértice oposto, estão alinhados.
|
|
|
|
|
|
|
Próximo: Como Dandelin demonstrou o Teorema de Pascal (I)
Anterior: Teorema de Pascal
Regresso ao Índice
|
|
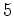 e
e  , movendo o vértice
, movendo o vértice 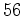 convergirá então para a recta
tangente à cónica
no ponto
convergirá então para a recta
tangente à cónica
no ponto 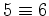 , e o hexagrama transforma-se num pentagrama
inscrito na cónica:
, e o hexagrama transforma-se num pentagrama
inscrito na cónica: e
e  .
.  convergirá para a recta
tangente no ponto
convergirá para a recta
tangente no ponto
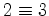 , e o hexagrama
transforma-se no tetragrama
, e o hexagrama
transforma-se no tetragrama 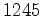 .
.  e
e 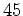 e,
e, 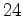 e
e 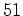 , bem como as tangentes
nos vértices opostos
, bem como as tangentes
nos vértices opostos  e
e 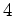 e ainda vértices
e ainda vértices