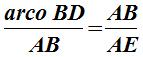Projecto POLYA







        Tarefa 7:                                                                                                  


        Analisando os movimentos que constroem a curva de Hípias, o que podes concluir sobre a

relação entre a amplitude dos arcos BD e P2D? 





        Como os movimentos que constroem a curva de Hípias são uniformes, existe uma 

proporcionalidade entre a distância percorrida pelo lado BC e a amplitude angular (medida

pelo arco) percorrida pelo lado AB: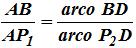 

“AB está para AP1 assim como o arco BD está para o arco P2D”

 






        Tarefa 8:                                                                                                  
    
          Agora que já sabes construir a curva de Hípias, podes usá-la para

trissectar o ângulo α.
  .
 

        






        Papo de Alexandria fez referência a Dinóstrato quando descreveu a curva. Dinóstrato foi 

um matemático ateniense que utilizou a curva na resolução de um problema geométrico, a 

rectificação da circunferência. Ele defendia que existia uma certa proporção na curva de Hípias: 





        Este resultado foi provado por Papo e foi tão importante que deu um novo nome à curva de Hípias: quadratriz.

         No século seguinte, Arquimedes de Siracusa estabelece a relação entre a quadratura do 

círculo e a rectificação da circunferência, construindo uma espiral.






        Tarefa 9:                                                                                                  

        Encontra uma imagem da espiral de Arquimedes e explica o que é que ele demonstrou para 

estabelecer a relação entre os dois problemas.

 





   

Regresso à página pricipal