Depois de
estudar algebricamente este problema, descobrimos
que o lado do quadrado me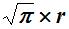de 
em que r é o raio
de circunferência. Conhecemos r,
e,
por isso, o problema de
construir o lado do quadrado é equivalente a podermos
construir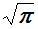 
com régua e compasso.
Relacionando a geometria com a álgebra, podemos
construir um número desta forma se este
for algébrico
(ou seja, se é solução de
uma equação polinomial*
com coeficientes inteiros
diferentes
de zero). É nesta altura que intervém o
matemático alemão Ferdinand von Lindemann,
que
demonstra que o número π não é
algébrico.
Assim,
ficou provado que também é impossível resolver
este problema.
|
 |
