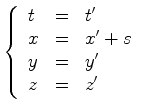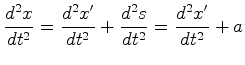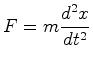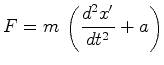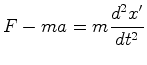Princípio da Relatividade Geral
 |
|||
Recorde que um
dos
princípios em que se baseia a teoria da
Relatividade Restrita é o chamado:
|
|||
|
Portanto,
os referenciais de
inércia têm um
estatuto
especial em Relatividade Restrita. Todos os
referenciais de inércia movem-se com velocidade uniforme uns
relativamente aos
outros. Mas, suponhamos agora que As
leis da Física são mais
complicadas em
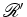 . Observadores em
. Observadores em 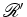 sentem forças
fictícias, ditas forças de inércia, que,
numa primeira
análise, não podem ser atribuídas a qualquer
agente directo.
Num referencial acelerado
sentem forças
fictícias, ditas forças de inércia, que,
numa primeira
análise, não podem ser atribuídas a qualquer
agente directo.
Num referencial acelerado 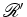 , a lei de inércia não é válida -
a velocidade de um corpo varia embora não haja qualquer
"força
real" que sobre ele actua!
, a lei de inércia não é válida -
a velocidade de um corpo varia embora não haja qualquer
"força
real" que sobre ele actua!
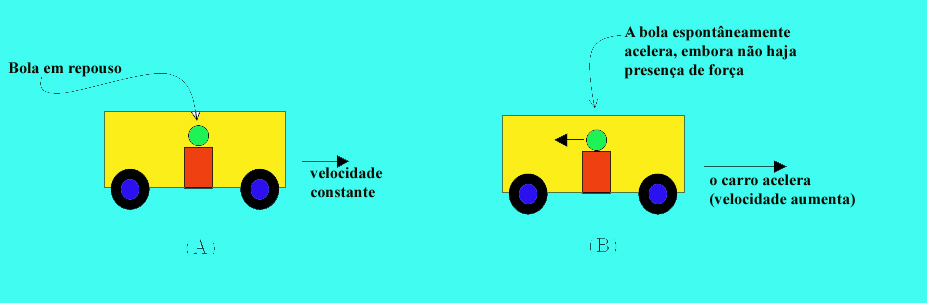 Figura 1 ... num referencial não inercial, os corpos estão sujeitos a pseudo-forças (forças de inércia) que, em princípio, não podem ser atribuídas a qualquer agente directo. |
|||
| |
Carro em movimento uniforme. A bola não se move |
||
|
Carro em movimento acelerado. A bola é puxada pela força de inércia |
|||
| Um Exemplo: |
|||
|
|||
 |
|||
|
Em Relatividade Restrita postula-se que as leis da Física devem ter a mesma forma em todos os referenciais de inércia. Estes referenciais desempenham pois um papel privilegiado relativamente a referenciais acelerados. No entanto, este estatuto especial dos referenciais de inércia era contrário à visão que Einstein tinha da realidade! Porque motivo a Natureza atribuiria um papel de privilégio aos referenciais de inércia? O facto de estar em movimento uniforme depende aliás do estado de movimento de quem observa. As leis da Física devem pois poder exprimir-se sob a mesma forma não importa qual o tipo de referencial. Nas próprias palavras de Einstein: "Que é que a Natureza tem a ver com os sistemas de coordenadas e respectivos estados de movimento? Afinal não sômos nós que os introduzimos para descrever matematicamente os fenómenos?". Na sua teoria da Relatividade Geral, Einstein generaliza o Princípio da Relatividade de Galileu, enunciando o seu:
É claro que esta é uma ideia completamente revolucionária, que parece contrariar algumas observações familiares. Quando estamos num carro que acelera somos empurrados para trás (figura 1). Parece difícil admitir que as leis da mecânica são as mesmas num referencial de inércia e num referencial acelerado. |
|||
Duas questões ainda:
Newton responde postulando a existência de um espaço absoluto - um espaço que existe independentemente de tudo, imutável, um palco absoluto no qual se desenrolam os acontecimentos naturais. Um observador inercial é pois, segundo Newton, aquele que está em repouso ou em movimento uniforme relativamente ao espaço absoluto. As forças de inércia ocorrem apenas para aqueles observadores que têm uma aceleração absoluta relativamente ao espaço absoluto. A experiência do balde de água, que descrevemos na secção seguinte, determina, segundo Newton, quando um sistema está em rotação absoluta relativamente ao espaço absoluto. |
|||
| Próximo: Princípio
de Mach Regresso ao Índice |
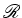 é um referencial de inércia e que
é um referencial de inércia e que 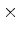 aceleração"
aceleração"