I. Leis de Newton. Referenciais de inércia |
|||
 |
Newton pensava no espaço físico como um recipiente vazio que continha toda a matéria do universo. Embora a matéria estivesse em constante movimento e mutação, o espaço era um contínuo ilimitado, infinito, fixo e inalterável. A Mecânica Clássica baseia-se nas três Leis de Newton seguintes, publicadas na sua grande obra "Principia Mathematica", em 1687:
Um referencial no qual seja válida a lei de inércia de Newton diz-se um referencial de inércia. Um observador em repouso num tal referencial diz-se um observador de inércia. Seja
A Relatividade restrita (ou especial) trata da descrição dos fenómenos por observadores de inércia e explica como se comparam as observações feitas por dois observadores de inércia em movimento relativo uniforme, um relativamente ao outro. |
||
| Página seguinte: transformações
de Galileu Índice |
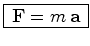
 um referencial
de inércia. Relativamente a
um referencial
de inércia. Relativamente a  um outro
referencial em movimento relativamente
a
um outro
referencial em movimento relativamente
a