|
|
|

|
- 1.
- Transformação de
Galileu
Um
acontecimento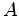 ocorre no instante
ocorre no instante 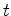 no ponto de coordenadas no ponto de coordenadas 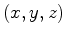 , relativas
a um referencial de inércia
, relativas
a um referencial de inércia  . Quais são as coordenadas
. Quais são as coordenadas 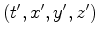 de de 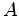 , relativas a um outro referencial de inércia
, relativas a um outro referencial de inércia  , que se move com
velocidade
, que se move com
velocidade 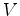 , relativamente a
, relativamente a  ?
?
Por simplicidade, supômos que o movimento
relativo se faz segundo
a direcção do eixo dos 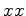 e que os eixos se mantêm sempre
paralelos. e que os eixos se mantêm sempre
paralelos.
A figura mostra que:
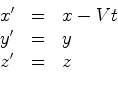 |
(2) |
equações às quais se deve
juntar:
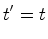 |
(3) |
que
traduz o carácter absoluto do tempo, de acordo com a
relatividade
de Galileu.
- 2.
- Invariância da
distância
Consideremos dois
pontos 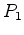 e e 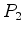 cujas coordenadas num
referencial de inércia cujas coordenadas num
referencial de inércia  são são 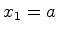 ,
, 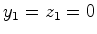 e e 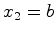 ,
, 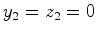 ,
respectivamente. A distância entre os dois pontos é igual
a
,
respectivamente. A distância entre os dois pontos é igual
a 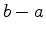 .
.
Seja
 um outro referencial
de inércia, que se move com velocidade um outro referencial
de inércia, que se move com velocidade 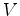 ,
relativamente a
,
relativamente a  , segundo a direcção do eixo dos
, segundo a direcção do eixo dos 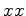 (os
eixos mantêm-se sempre paralelos). (os
eixos mantêm-se sempre paralelos).
Relativamente a este referencial os pontos 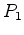 e e 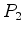 movem-se - as
equações do movimento são obtidas usando as
transformações
(2) e (3): movem-se - as
equações do movimento são obtidas usando as
transformações
(2) e (3):
-
-
-
Suponhamos agora que
observadores em  medem a posição do
ponto medem a posição do
ponto 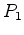 no instante no instante 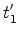 e a do ponto e a do ponto 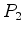 no instante no instante 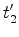 . A diferença das duas leituras é:
. A diferença das duas leituras é:
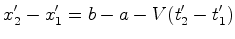 -
Portanto, se 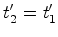 , vemos que
, vemos que 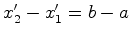 , isto é:
, isto é:
A
separação espacial entre dois acontecimentos que ocorrem
no mesmo
instante (são simultâneos) é invariante.
Veremos
que isto
não é verdadeiro em relatividade de Einstein.
- 3.
- Transformação
das velocidades
-
-
Suponhamos
que um ponto se move numa recta com velocidade uniforme 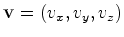 , medida num referencial de inércia
, medida num referencial de inércia  . Se o ponto parte da
origem no instante
. Se o ponto parte da
origem no instante  , as equações do movimento são:
, as equações do movimento são:
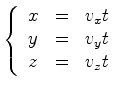 |
(4) |
Seja
 um outro referencial
de inércia, que se move com velocidade um outro referencial
de inércia, que se move com velocidade 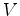 ,
relativamente a
,
relativamente a  , segundo a direcção do eixo dos
, segundo a direcção do eixo dos 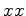 (os
eixos mantêm-se sempre paralelos). (os
eixos mantêm-se sempre paralelos).
Usando as
transformações (2) e (3) para exprimir 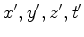 em termos de em termos de 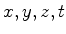 , obtemos:
, obtemos:
isto é:
-
Estas
equações descrevem um movimento rectílineo
uniforme com
velocidade constante 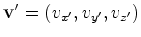 ,
onde: ,
onde:
-
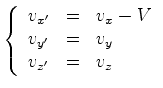 |
(5) |
- 4.
- Invariância
da aceleração
-
De acordo com as equações (5), as velocidades do
movimento do ponto diferem de uma constante 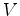 . Portanto as
acelerações são as mesmas em ambos os
referenciais:
. Portanto as
acelerações são as mesmas em ambos os
referenciais:
-
Vejamos um exemplo sugestivo de aplicação
das fórmulas que
acabamos de referir, e que será útil em breve.
|
|
Exemplo:
|
Dois nadadores nadam num rio de largura 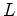 . A corrente da água do rio
tem velocidade . A corrente da água do rio
tem velocidade 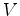 relativamente a um referencial relativamente a um referencial  , fixo
nas margens do rio.
, fixo
nas margens do rio. Cada
nadador nada com velocidade 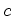 relativamente ao referencial de
repouso, relativamente ao referencial de
repouso,  , da água (o referencial que se move solidário
com a corrente, da esquerda para a direita no applett ...).
, da água (o referencial que se move solidário
com a corrente, da esquerda para a direita no applett ...).
O nadador 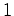 atravessa o rio, partindo de um ponto atravessa o rio, partindo de um ponto 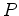 da margem
para o ponto oposto da margem
para o ponto oposto 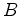 , na outra margem, e depois regressa ao ponto
de partida. O nadador
, na outra margem, e depois regressa ao ponto
de partida. O nadador 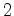 nada uma distância nada uma distância 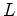 , paralelamente
à margem (e relativamente a esta), até ao ponto
, paralelamente
à margem (e relativamente a esta), até ao ponto 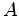 , e depois
regressa.
, e depois
regressa.
Quem ganha a prova ?
|
|
|
Animação
1: Mova com o rato o ponto de controlo para obter a
resposta.
|
|
Resolução:
|
As coordenadas dos dois referenciais
relacionam-se através das equações:
 |
(6) |
(o sinal de 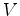 é é 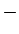 porque
supômos que a corrente se desloca da esquerda para a direita, na
direcção dos porque
supômos que a corrente se desloca da esquerda para a direita, na
direcção dos 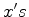 positivos). positivos).
No
referencial  (referencial de
repouso da
água) ambos os nadadores
nadam com velocidade (referencial de
repouso da
água) ambos os nadadores
nadam com velocidade 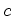 em qualquer direcção. Mas no
referencial em qualquer direcção. Mas no
referencial  (referencial fixo às margens) a situação
altera-se. A relação
entre as componentes da velocidade nos dois referenciais obtem-se
derivando as relações anteriores relativamente ao tempo
(lembrando que
(referencial fixo às margens) a situação
altera-se. A relação
entre as componentes da velocidade nos dois referenciais obtem-se
derivando as relações anteriores relativamente ao tempo
(lembrando que  ) e já foi obtida na secção anterior:
) e já foi obtida na secção anterior:
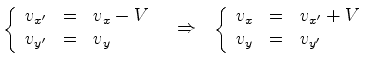 |
(7) |
Vejamos o tempo do percurso do nadador  : :
Relativamente a  ele nada uma
distância ele nada uma
distância 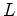 ao longo da margem, como na
animação 1, com uma velocidade ao longo da margem, como na
animação 1, com uma velocidade 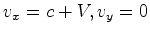 e depois regressa
com uma velocidade e depois regressa
com uma velocidade  (é claro que
estamos a
supôr que (é claro que
estamos a
supôr que 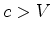 !). O tempo total gasto é pois:
!). O tempo total gasto é pois:
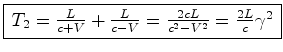 |
(8) |
onde:
 |
(9) |
é o chamado Factor de Lorentz.
Vejamos agora o
tempo
do percurso do nadador 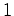 : :
As
componentes da velocidade do nadador 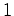 , no referencial
, no referencial  , são
, são 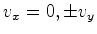 , para
algum valor , para
algum valor 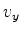 que se pretende
determinar
(o sinal + no percurso que se pretende
determinar
(o sinal + no percurso  e o sinal - no percurso de regresso e o sinal - no percurso de regresso 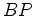 ). ).
Mas,
segundo o referencial  , que se move solidário com a
corrente, o nadador
, que se move solidário com a
corrente, o nadador  percorre uma trajectória oblíqua: percorre uma trajectória oblíqua:
com
velocidade:
isto é:
O tempo total gasto pelo nadador  é pois igual a: é pois igual a:
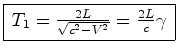 |
(10) |
Temos portanto que:
Se 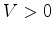 o nadador o nadador 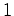 ganha a corrida. Se ganha a corrida. Se  , isto
é, se a água está parada (não há
corrente), ambos chegam
ao mesmo tempo.
, isto
é, se a água está parada (não há
corrente), ambos chegam
ao mesmo tempo.
E se a corrente faz um ângulo de 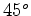 relativamente aos dois
nadadores ? relativamente aos dois
nadadores ?
|
|
|
|
|
|
Página seguinte: Experiência
de Michelson-Morley
Página
anterior: Leis de Newton e referenciais de inércia
Índice
|
|

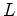 . A corrente da água do rio
tem velocidade
. A corrente da água do rio
tem velocidade 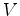 relativamente a um referencial
relativamente a um referencial  , fixo
nas margens do rio.
, fixo
nas margens do rio. 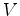 é
é 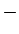 porque
supômos que a corrente se desloca da esquerda para a direita, na
direcção dos
porque
supômos que a corrente se desloca da esquerda para a direita, na
direcção dos 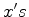 positivos).
positivos). 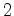 :
: ele nada uma
distância
ele nada uma
distância 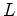 ao longo da margem, como na
animação 1, com uma velocidade
ao longo da margem, como na
animação 1, com uma velocidade 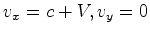 e depois regressa
com uma velocidade
e depois regressa
com uma velocidade  (é claro que
estamos a
supôr que
(é claro que
estamos a
supôr que 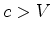 !). O tempo total gasto é pois:
!). O tempo total gasto é pois: 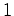 :
: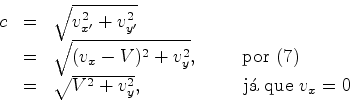
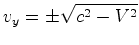
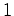 é pois igual a:
é pois igual a:

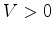 o nadador
o nadador 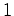 ganha a corrida. Se
ganha a corrida. Se  , isto
é, se a água está parada (não há
corrente), ambos chegam
ao mesmo tempo.
, isto
é, se a água está parada (não há
corrente), ambos chegam
ao mesmo tempo. 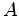 ocorre no instante
ocorre no instante 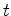 no ponto de coordenadas
no ponto de coordenadas 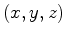 , relativas
a um referencial de inércia
, relativas
a um referencial de inércia 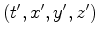 de
de  , que se move com
velocidade
, que se move com
velocidade  e que os eixos se mantêm sempre
paralelos.
e que os eixos se mantêm sempre
paralelos. 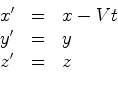
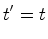
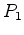 e
e 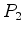 cujas coordenadas num
referencial de inércia
cujas coordenadas num
referencial de inércia 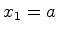 ,
, 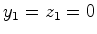 e
e 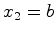 ,
, 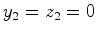 ,
respectivamente. A distância entre os dois pontos é igual
a
,
respectivamente. A distância entre os dois pontos é igual
a 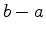 .
. 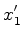
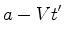
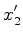

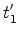 e a do ponto
e a do ponto 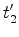 . A diferença das duas leituras é:
. A diferença das duas leituras é: 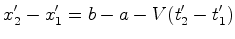
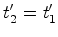 , vemos que
, vemos que 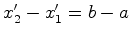 , isto é:
, isto é:
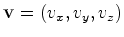 , medida num referencial de inércia
, medida num referencial de inércia  , as equações do movimento são:
, as equações do movimento são: 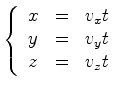
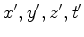 em termos de
em termos de 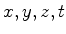 , obtemos:
, obtemos: 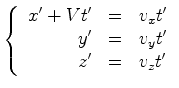
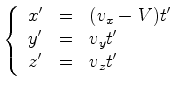
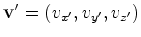 ,
onde:
,
onde: 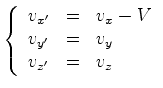
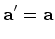
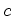 relativamente ao referencial de
repouso,
relativamente ao referencial de
repouso, 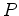 da margem
para o ponto oposto
da margem
para o ponto oposto  , na outra margem, e depois regressa ao ponto
de partida. O nadador
, na outra margem, e depois regressa ao ponto
de partida. O nadador 
 ) e já foi obtida na secção anterior:
) e já foi obtida na secção anterior: 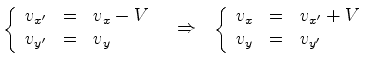
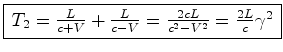

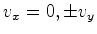 , para
algum valor
, para
algum valor 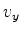 que se pretende
determinar
(o sinal + no percurso
que se pretende
determinar
(o sinal + no percurso 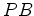 e o sinal - no percurso de regresso
e o sinal - no percurso de regresso 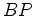 ).
). 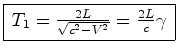
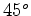 relativamente aos dois
nadadores ?
relativamente aos dois
nadadores ?