Relatividade Restrita - Uma introdução
Os ``Paradoxos" |
||
Um paradoxo é uma aparente inconsistência ou contradição numa teoria. Se o paradoxo não puder ser resolvido de forma satisfatória, a teoria falha e deve ser modificada ou abandonada. |
||
A vara e o celeiro |
||
|
Dois camponeses têm um celeiro com comprimento próprio:

no seu referencial de
repouso
 .
Os camponeses estão, um no lado esquerdo e o outro no lado
direito
do celeiro. As portas estão abertas.
.
Os camponeses estão, um no lado esquerdo e o outro no lado
direito
do celeiro. As portas estão abertas. Um corredor transporta uma vara com comprimento próprio:
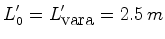 no seu referencial de repouso  .
.
O corredor aproxima-se
do celeiro com uma velocidade
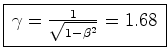
De acordo com a ``contracção" dos comprimentos, os camponeses pensam que a vara tem comprimento:
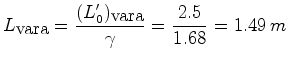
Mas, por outro lado, o corredor pensa que o celeiro tem:
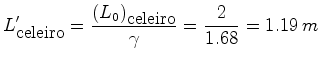
Portanto:
Vamos construir um diagrama de Minkowski para esta experiência. Para isso consideremos os acontecimentos seguintes:
Relativamente
aos camponeses, no seu referencial de repouso
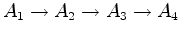
uma vez que
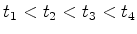 . Por outro lado, relativamente ao
corredor, no seu referencial de repouso
. Por outro lado, relativamente ao
corredor, no seu referencial de repouso  , a sequência temporal
dos mesmos acontecimentos é:
, a sequência temporal
dos mesmos acontecimentos é:
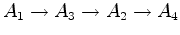
Daí
que existe um intervalo de tempo, medido em Não há qualquer paradoxo !!
Ambas as descrições são
válidas !!
|
||
Os gémeos |
||
|
A figura seguinte mostra
as linhas de universo de duas naves espaciais -
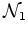 ,
que parte da terra à velocidade ,
que parte da terra à velocidade 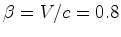 e e 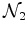 que regressa à terra com a mesma velocidade:
que regressa à terra com a mesma velocidade:
A
linha de universo da terra é o eixo dos As marcas nas linhas de
universo de cada uma das naves representam
intervalos de um ano, de acordo com relógios nas naves. Note que
elas se encontram a uma distância uma das outras superior
à das
marcas do eixo dos A
nave Isto
é consistente com o facto de que, do ponto de vista dos
habitantes da terra, o relógio dos astronautas anda mais devagar
por um factor igual a O
applett seguinte ilustra o facto de que, do ponto de vista do
astronauta, os relógios da terra andam mais devagar durante a
viagem. Quando ele deixa o referencial de
Esta
linha A análise, do ponto
de vista do astronauta, está representada no
applett seguinte:
As
linhas amarelas representam as trajectórias de sinais luminosos
emitidos pela terra, um por cada ano terrestre. Quando
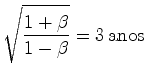 enquanto que a taxa à qual são recebidos pela nave 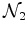 é
de:
é
de:
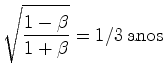 como se viu quando estudamos o efeito Doppler. Portanto
a nave Por
outro lado, no applett seguinte as linhas amarelas
representam as trajectórias de sinais luminosos emitidos pelo
astronauta, um por ano. Na terra eles são vistos com a mesma
frequência - cada 3 anos para os que são emitidos pela
nave
|
||
| Página seguinte: Referências Página anterior: Diagramas de Minkowski Índice |
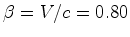 . O
factor de Lorentz é pois igual a:
. O
factor de Lorentz é pois igual a: 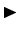
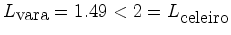
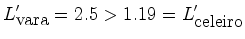
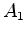 .
.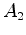 .
.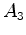 .
.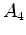 .
.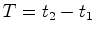 em que
a vara está completamente dentro do celeiro,
o que não acontece quando a experiência é descrita
em
em que
a vara está completamente dentro do celeiro,
o que não acontece quando a experiência é descrita
em 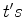 e as marcas
representam intervalos de um ano. Dez anos passaram na terra entre a
partida de
e as marcas
representam intervalos de um ano. Dez anos passaram na terra entre a
partida de 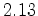 (porquê ?).
(porquê ?).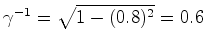 .
. 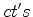 no
ponto
no
ponto 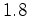 anos (
anos (
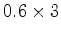 ).
Imediatamente após mudar de
nave, para o regresso, o astronauta novamente lê o tempo da terra
traçando agora a linha de
).
Imediatamente após mudar de
nave, para o regresso, o astronauta novamente lê o tempo da terra
traçando agora a linha de 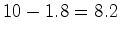 anos. A
diferença
anos. A
diferença 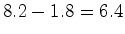 anos
é
varrida pela linha de simultaneidade quando o astronauta efectua a
mudança da nave
anos
é
varrida pela linha de simultaneidade quando o astronauta efectua a
mudança da nave 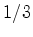 de ano quando
são emitidos por
de ano quando
são emitidos por