Relatividade Restrita - Uma introdução
Diagramas de Minskowski |
||
 |
||
|
Uma partícula que
percorre o eixo dos
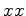 com velocidade
constante com velocidade
constante 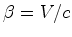 , será representada pela sua linha de universo que, neste
caso, é a recta:
, será representada pela sua linha de universo que, neste
caso, é a recta: 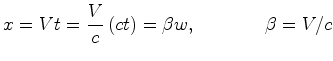 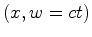 .
.
Vejamos
agora como se representa o referencial
Como se traça o eixo 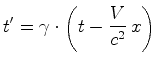 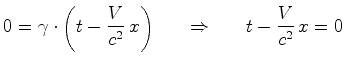 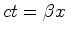 é
a equação do eixo
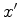 (note que ele tem a mesma
inclinação
relativamente ao eixo dos (note que ele tem a mesma
inclinação
relativamente ao eixo dos 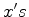 , que o eixo
, que o eixo 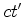 tem relativamente
ao eixo dos tem relativamente
ao eixo dos 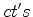 .
. Traçando
a hipérbole |
||
| Comprimento próprio |
Definimos o comprimento
próprio de um objecto, num dado
referencial
 , como sendo a separação espacial entre os acontecimentos
que representam as respectivas extremidades, medidas
simultâneamente, isto é, os dois acontecimentos devem
estar numa mesma
linha de simultaneidade do referencial
, como sendo a separação espacial entre os acontecimentos
que representam as respectivas extremidades, medidas
simultâneamente, isto é, os dois acontecimentos devem
estar numa mesma
linha de simultaneidade do referencial  . . O comprimento
próprio é pois o
comprimento medido no referencial de repouso do objecto. É o
maior
comprimento medido por um observador. Qualquer outro observador
mede um comprimento menor.
Note que não se afirma que qualquer objecto se contrai fisicamente, quando se move. A medição é menor porque os observadores não têm a mesma noção de simultaneidade. Portanto, apesar de ser usual o termo de "contracção dos comprimentos", o que de facto acontece é um desacordo àcerca da noção de simultaneidade e não uma contracção física dos objectos. |
|
| Intervalo de tempo próprio |
O intervalo de tempo
próprio entre dois acontecimentos, medido
relativamente a um referencial
 , define-se como sendo a separação
temporal dos dois acontecimentos, medida num relógio em repouso
relativamente a esses acontecimentos. Portanto, os dois acontecimentos
têm lugar no
mesmo sítio, de acordo com o observador que transporta o
referido
relógio.
, define-se como sendo a separação
temporal dos dois acontecimentos, medida num relógio em repouso
relativamente a esses acontecimentos. Portanto, os dois acontecimentos
têm lugar no
mesmo sítio, de acordo com o observador que transporta o
referido
relógio. Consideremos
agora um sistema em repouso, relativamente a um
observador O tempo próprio
deste sistema é a separação temporal Como
pode ser visto no applett, a separação temporal
relativamente a um observador 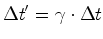 Portanto o tempo próprio é o menor tempo medido. |
|
| Página seguinte: Os "Paradoxos" Página anterior: Transformações de Lorentz Índice |
 , no diagrama de Minskowski do referencial
, no diagrama de Minskowski do referencial 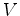 relativamente ao referencial
relativamente ao referencial 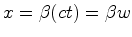 é a linha de universo do relógio do
observador
é a linha de universo do relógio do
observador 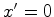 , esta linha pode ser
tomada como o eixo dos
, esta linha pode ser
tomada como o eixo dos 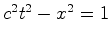 . Pontos nesta
curva devem satisfazer também a equação
. Pontos nesta
curva devem satisfazer também a equação 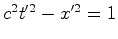 , por
invariância do intervalo. Portanto, a intersecção
desta
hipérbole com o eixo dos
, por
invariância do intervalo. Portanto, a intersecção
desta
hipérbole com o eixo dos 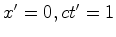 . Esta intersecção dá pois a unidade de
medida ao longo do eixo
. Esta intersecção dá pois a unidade de
medida ao longo do eixo 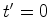 . Substituindo em (
. Substituindo em (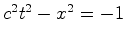 , calibramos o eixo dos
, calibramos o eixo dos 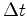 entre os acontecimentos
entre os acontecimentos 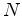 (Nascimento) e
(Nascimento) e 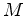 (Morte),
medida por um relógio em repouso relativamente ao referido
sistema.
(Morte),
medida por um relógio em repouso relativamente ao referido
sistema.