Cónicas - Velhas Questões - Novas Abordagens
Cónicas - Velhas Questões - Novas Abordagens
|
CÓNICAS
Velhas Questões - Novas
|
 |
Rosa Ribeiro Céu Silva
CMUP - DMPUP
|
Na Grécia Antiga
as cónicas eram obtidas seccionando um cone por um plano.

Na teoria de Menecmo
são utilizados cones rectos
e os planos de secção são perpendiculares a uma
geratriz.
De acordo com o
ângulo no vértice
do cone assim a cónica obtida é:
|
oxitomo
(ângulo, no vértice do cone, |
 |
|
ortotomo (ângulo, no
|
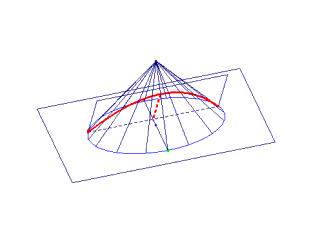 |
|
amblitomo
(ângulo, no vértice do cone,
|
 |
Apolónio estudou as
cónicas numa perspectiva que se aproxima da actual.
Apolónio utiliza
cones de base circular de
duas folhas e planos de
secção que intersectam a base do cone segundo rectas perpendiculares ao
triângulo axial.
Conforme posição
relativa do plano secante e do triângulo axial assim:
|
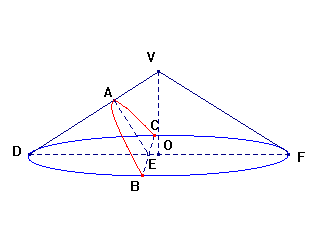
elipse (plano secante
|
 |
|
parábola (plano secante
|
 |
|
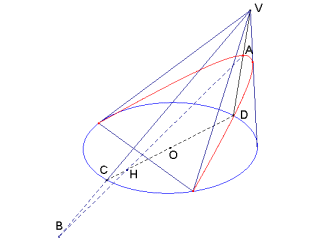
hipérbole (plano secante
|
 |
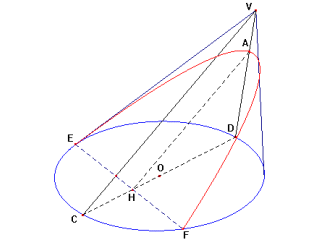
Para cada cónica
indicou um sintoma
(propriedade característica da cónica) que envolve elementos dos três planos
intervenientes na obtenção da cónica:
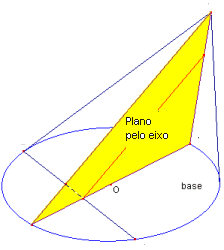
-
o plano da base do cone
-
o plano de secção
-
o plano do
triângulo axial
Sintoma da
parábola
"Se um cone é cortado por um plano
que passa pelo eixo e por um outro plano que corta a base do cone segundo uma
recta perpendicular à base do triângulo passando pelo eixo; se, além disso, o
diâmetro da secção é paralelo a um dos lados do triângulo que passa pelo eixo, o
quadrado de qualquer recta conduzida da secção do cone paralelamente à secção
comum do plano secante e da base do cone até ao diâmetro da secção equivale ao
rectângulo delimitado pela recta que ela corta sobre o diâmetro, do lado do
vértice da secção, e por uma certa recta cuja razão para a recta situada entre o
ângulo do cone e o vértice da secção é a mesma que a do quadrado da base do
triângulo passando pelo eixo para a do rectângulo delimitado pelos dois outros
lados do triângulo. Chamaremos tal secção uma parábola"
(Ver Eecke, Les Coniques d’Apollonius de
Perge, p.21).
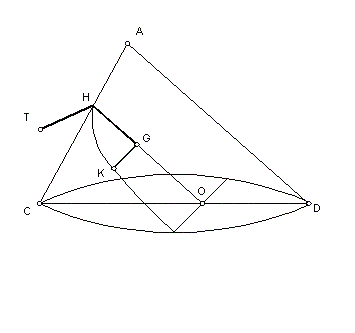
A propriedade
definidora da parábola pode traduzir-se pela relação
![]()
com 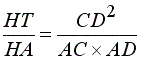
-
H
é o vértice da parábola
- ponto de intersecção do plano de secção com o lado do
triângulo axial -
HO
é o eixo da parábola
- recta definida pelo vértice da parábola e pelo ponto de intersecção do plano
de secção com a base do triângulo axial - latus transversum -
K
é um ponto qualquer da curva e
G
é o seu projectado ortogonal sobre o eixo da parábola -
HT
é o latus erectum - latus rectum -
parâmetro

(Apolónio,
Cónicas, III, 2- 4, manuscrito de 1536 feito para o Papa Paulo III)
As
páginas acima dizem respeito à
igualdade de áreas de triângulos e
quadriláteros formados por tangentes e diâmetros das cónicas e por tangentes e
paralelas às tangentes.
Apolónio, Cónicas, I, 42
Quando uma recta
(t)
tangente a uma parábola encontra um diâmetro
(em D)
se do ponto de contacto
(T)
baixarmos um recta
(r)
de modo ordenado sobre o diâmetro e se de um ponto
(X)
qualquer da secção tirarmos uma recta paralela à tangente
(t')
e outra
(r')
paralela à recta baixada do ponto de contacto, a área do triângulo formado por
estas duas últimas rectas é igual à área do paralelogramo compreendido entre
a recta baixada do ponto de contacto
e a recta
(r')
que corta a paralela a essa, pelo vértice da secção.
(trad. Paul ver EecKe)
Por t ser tangente à parábola e TE ser "conduzida de modo ordenado" é VD=DE
logo ED=2VE, portanto
área TED = área VETA
Por serem T e X pontos da parábola é TE2=2pVE
e CX2=2pVC,
portanto
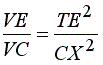
Como
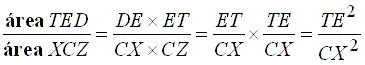
e 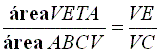
vem
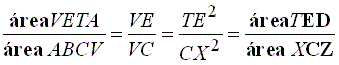
logo
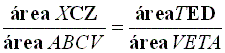
Como
![]()
Conclui-se que
![]()
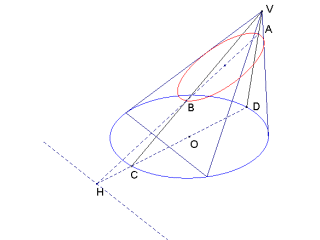
Apolónio, Cónicas, III, 1
Quando rectas tangentes
(BD e CE)
a uma secção do cone [ou
a uma circunferência do círculo] se encontram, e se, pelos seus pontos de
contacto
(B e E)
traçarmos diâmetros
(BC e ED)
encontrando as tangentes
(em C e D), os triângulos assim
obtidos
(CAB e EAD), dispostos segundo o respectivo vértice
(A), são iguais.
BZ
// CE
logo BZEC é um paralelogramo de área
igual à de BDZ pois DZ=2EZ (Cónicas, I,35)
Retirando ao triângulo
BDZ e ao paralelogramo BZEC o
quadrilátero comum BZEA, conclui-se que
CAB e EAD
latus erectum
O
latus erectum,
era um segmento obtido por um processo de
aplicação de áreas
dado por uma expressão dependente do triângulo axial e do vértice da parábola,
do seguinte modo:
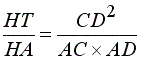
Como interpretar
geometricamente o
latus erectum?
Em finais do século XVII, Jacques Bernoulli deduziu um processo simples de
reconhecer geometricamente, no cone gerador, um segmento de comprimento igual ao
do parâmetro, tomando como suporte a definição de parábola dada por Apolónio
(Apolónio, Conicas, Livro I,
proposição XI).

(Jacques
Bernoulli, finais do séc. XVII, Obra completa, vol. I, pp. 45 e 46)
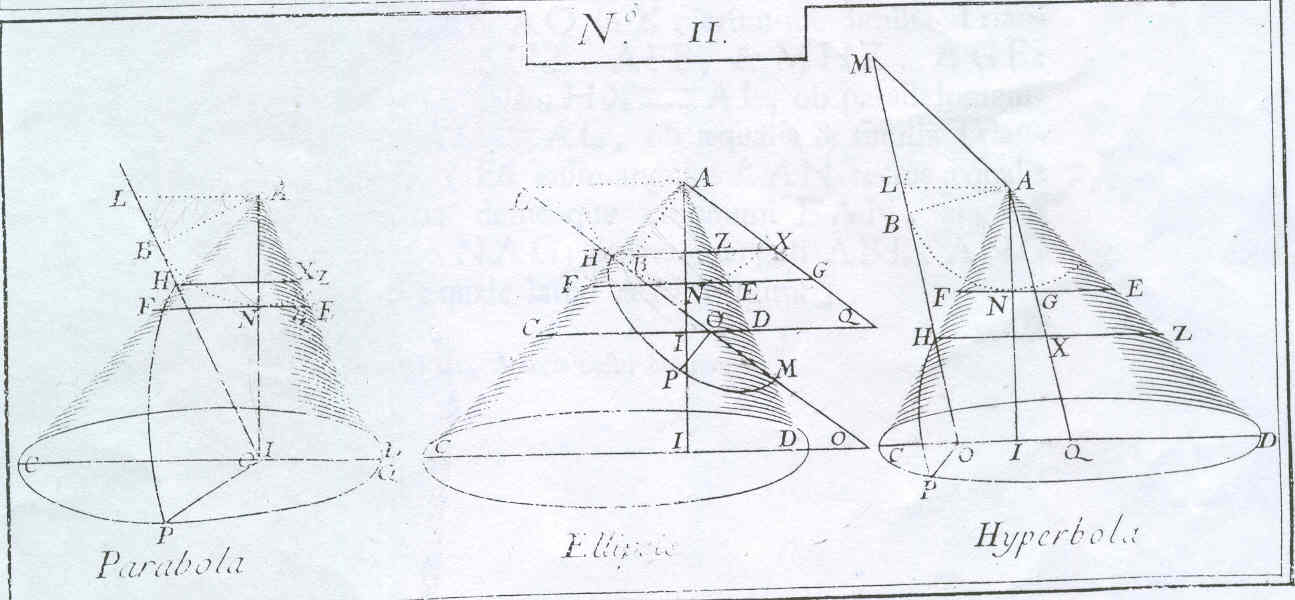
Novum Theorema
Pro Doctrina Sectionum Conicarum
"Tomando um plano paralelo à base de
um cone e situado à mesma distância do seu vértice que o plano da secção cónica,
este plano intersectará o cone segundo um círculo cujo diâmetro será o latus
rectum da cónica".
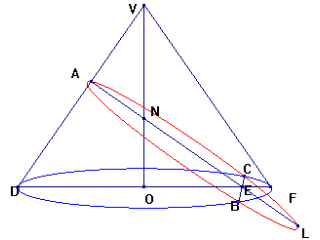
Parábola - Esboço
da demonstração
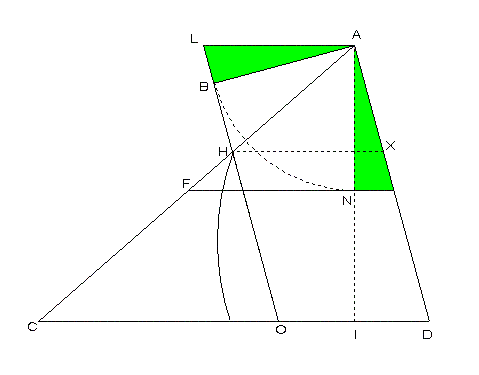 ^
^
s -
plano da base do cone
a -
plano de secção ACD -
triângulo axial
HO o eixo da parábola AI
^ s
AB
^ HO
Tomemos N
em AI, tal que
![]()
Seja
b um plano paralelo a
s
passando por N. O plano
b intersecta o
triângulo axial ACD nos pontos F e E, que são as extremidades do diâmetro do
círculo produzido na superfície cónica pelo plano
b.
Mostraremos que FE é o latus
rectum.
LA
//
CD, com LÎHO;
HX //
CD, com XÎAD
-
ABL
@
ANE (AB=NA,
const., ÐABL=
ÐANE
= 90, ÐLAB=ÐEAN,
pq ÐLAB=
ÐLAN
- ÐBAN
=ÐEAB
- ÐNAB=ÐEAN).
Logo
LA = AE. -
HXAL é um paralelogramo
(pq HX//LA
e HL//XA).
Logo HX=LA.
Donde, LA=AE e HX=LA, portanto
HX=AE.
AHX
»
AFE »
ACD (ângulos iguais cada um a cada
um), vem
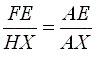
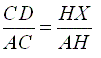
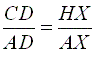
(2)
(3) (4)
De (2) e HX=AE
vem
![]()
De
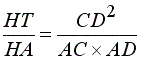
e HX = AE resulta
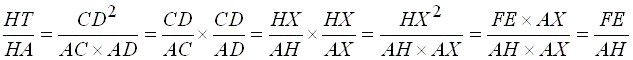
Logo
HT=FE
"Apolónio e os geómetras que
escreveram depois dele, deram diferentes expressões geométricas, tomadas no
cone, do comprimento do latus rectum, para cada secção, mas nenhuma nos
pareceu tão simples e tão elegante como a de Jacques Bernoulli."
(Chasles, Aperçu Historique des Méthodes
en Géométrie, p.19)
http://perso.wanadoo.fr/alta.mathematica/apollonius.html
Bibliografia
-
Bernoulli, Jacques. Obra completa, vol I, Lips, 1699. -
Chasles, M. Aperçu Historique sur
l’Origine et le Développement des Méthodes en Géométrie. Paris, Gauthier-Villars
et Fils, Imprimeurs-Libraires, 1889. -
Eves, H. Introdução à História da Matemática -
trad. Hygino H. Domingues. Campinas, S.P.: Editora da UniCamp, 1995. -
Heath, T. Apollonius of Perga –
Treatise on Conic Sections. Cambridge: at the University Press, 1896. -
Katz, V. A History of Mathematics:
An Introduction. New York: Harper Collins College Publishers, 1993. -
Veloso, E. Geometria, Temas Actuais. Lisboa:
Instituto de Inovação Educacional, 1998. -
Veloso, E, H. Fonseca, J. P. Ponte e P. Abrantes.
Ensino da Geometria no virar do milénio. Departamento de Educação da
Faculdade de Ciências da Universidade de Lisboa, 1999.
Ver Eecke, P. Les Coniques d’Apollonius de
Perge-Oeuvres traduites pour la Première fois du grec en français, avec une
introdution et des notes. Bruges, Desclée, de Brouwer et C., 1923.

