Exemplo 3. Três barras
O sistema articulado mais simples
é constituído por 4 barras,
formando um quadrilátero, articulado nos seus vértices.
Este
sistema tem um ou dois graus de liberdade conforme fixamos dois ou
apenas um dos pontos ligados ao sistema.
Quando os dois pontos
fixos coincidem com duas das articulações
temos o que se chama um 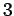 -barras. As barras
-barras. As barras 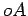 e
e 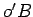 dizem-se as manivelas
e a barra
dizem-se as manivelas
e a barra  a biela.
a biela.
Os pontos  e
e 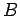 movem-se em círculos de raios
movem-se em círculos de raios 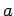 e
e 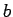 ,
respectivamnte, mas, em geral, não os descrevem
completamente. No applet pode redimensionar os comprimentos das
barras e verificar
o comportamento do sistema controlando com o rato o ponto
,
respectivamnte, mas, em geral, não os descrevem
completamente. No applet pode redimensionar os comprimentos das
barras e verificar
o comportamento do sistema controlando com o rato o ponto  .
.
Se o ponto 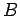 em vez de estar ligado ao ponto
fixo
em vez de estar ligado ao ponto
fixo  , estiver
restrito a mover-se sobre uma recta que passa em
, estiver
restrito a mover-se sobre uma recta que passa em  , temos (supondo
que
, temos (supondo
que 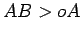 ) a
biela-manivela usuais, que serve para transformar um
movimento rectilíneo periódico de
) a
biela-manivela usuais, que serve para transformar um
movimento rectilíneo periódico de 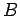 , num movimento circular
contínuo do ponto
, num movimento circular
contínuo do ponto  , ou vice-versa.
, ou vice-versa.
Se as manivelas
são iguais entre si e a biela  é igual à
distância
é igual à
distância 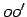 dos pontos fixos, mas formando um
contra-paralelogramo, como no applett seguinte, as curvas descritas
por um qualquer ponto rigidamente ligado à biela são do
quarto grau. No applet, o ponto médio do segmento
dos pontos fixos, mas formando um
contra-paralelogramo, como no applett seguinte, as curvas descritas
por um qualquer ponto rigidamente ligado à biela são do
quarto grau. No applet, o ponto médio do segmento descreve uma lemniscata de Bernoulli.
descreve uma lemniscata de Bernoulli.
É fácil obter, em cada instante, as normais às
trajectórias
dos pontos rigidamente ligados à biela. De facto estas normais
passam todas pelo centro instantâneo de rotação,
que está situado no ponto de encontro das
normais 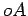 e
e 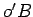 às trajectórias de
às trajectórias de  e
e 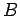 .
.
Olhando para o applet anterior, vemos que:
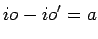
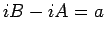
A primeira destas igualdades diz-nos que o lugar geométrico do
centro instantâneo de rotação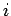 , no plano fixo
, no plano fixo  , é uma hipérbole cujos
focos
são
, é uma hipérbole cujos
focos
são  e
e  . Por outro lado, a segunda igualdade diz-nos que
o
lugar geométrico do centro instantâneo de
rotação
. Por outro lado, a segunda igualdade diz-nos que
o
lugar geométrico do centro instantâneo de
rotação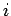 , agora no plano móvel
, agora no plano móvel
 (suposto ligado à biela
(suposto ligado à biela  ), é uma hipérbole igual à
primeira e cujos focos são
), é uma hipérbole igual à
primeira e cujos focos são  e
e 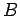 . Portanto o movimento
. Portanto o movimento
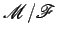 , no
caso em que a biela é mais longa que as manivelas,
é o movimento de rolamento de uma hipérbole (a rolante)
em
, no
caso em que a biela é mais longa que as manivelas,
é o movimento de rolamento de uma hipérbole (a rolante)
em
 , sobre uma outra igual (a base) em
, sobre uma outra igual (a base) em
 .
.
Quando a biela é mais curta que as manivelas, o movimento é o do rolamento de uma elipse (a rolante) em
 , sobre uma
outra igual (a base) em
, sobre uma
outra igual (a base) em  .
.
Consideremos a
posição do sistema na qual as manivelas são
paralelas. O centro instantâneo de rotação
está então no infinito, na direcção
comum destas rectas, e todo o ponto ligado à biela  tem um
deslocamento infinitesimal equivalente a uma translacção
perpendicular à direcção comum de
tem um
deslocamento infinitesimal equivalente a uma translacção
perpendicular à direcção comum de 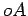 e
e 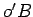 . Em particular, o
ponto médio
. Em particular, o
ponto médio 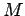 de
de  passa, sobre a sua trajectória, por um
ponto de inflexão em que a tangente é perpendicular a
passa, sobre a sua trajectória, por um
ponto de inflexão em que a tangente é perpendicular a 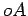 (faça o teste no applet ...)
(faça o teste no applet ...)
Watt observou que, para um comprimento das bielas muito
grande quando comparado com o comprimento da biela, o ponto 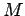 afasta-se pouco desta tangente e a sua trajectória diz-se, por
isso, uma curva de longa inflexão. Deduziu assim uma
solução
aproximada para a transformação, sem guiagem, de um
movimento
circular (o do ponto
afasta-se pouco desta tangente e a sua trajectória diz-se, por
isso, uma curva de longa inflexão. Deduziu assim uma
solução
aproximada para a transformação, sem guiagem, de um
movimento
circular (o do ponto  ) em movimento rectilíneo (o do ponto
) em movimento rectilíneo (o do ponto 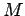 ).
).
Para ter, fora da recta  , um ponto que descreva uma recta, ele
construiu sobre
, um ponto que descreva uma recta, ele
construiu sobre  e sobre o segmento
e sobre o segmento 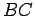 , que prolonga
, que prolonga 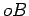 , de
um comprimento igual, um paralelogramo articulado
, de
um comprimento igual, um paralelogramo articulado 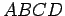 :
:
A recta 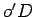 passa pelo ponto médio
passa pelo ponto médio 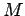 de
de  e
e 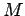 é o
ponto médio de
é o
ponto médio de 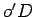 . A trajectória de
. A trajectória de 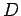 é pois
homotética, relativamente a
é pois
homotética, relativamente a  , da trajectória de
, da trajectória de 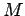 , e é
por isso também uma curva de longa inflexão.
, e é
por isso também uma curva de longa inflexão.
Existem muitos outros
processos de traçado aproximado e exacto de
uma linha recta usando sistemas articulados. Para uma
descrição
detalhada veja a tradução da obra de Kempe "Como
desenhar uma linha recta, usando sistemas articulados".
Next: Método de Mannheim ... Previous: Exemplo 2. Um ângulo Contents Joao Nuno Tavares 2005-04-12