| |
Next: About this document ... Previous: 3-Barras Contents |
||
|
|
|||
Método de Mannheim para a determinação do centro de curvatura
Created with Cinderella |
|||
|
Anàlogamente, o ângulo em
Mas o mesmo acontece para o ângulo em
Anàlogamente o ponto característico Mas isto
significa que o centro instantâneo de rotação do
ângulo Logo, unindo
Apliquemos esta teoria ao
caso especial em que o triângulo dado
degenera num segmento de recta com um ponto no seu interior. |
|||
Created with Cinderella |
|||
|
Obtemos assim a seguinte construção:
Dado um segmento
Para construir a normal à trajectória de
Aplicamos agora a proporção (1)
- sobre o segmento
Inversamente, suponhamos que uma recta se desloca de tal forma que
três curvas dadas Para obter o
ponto característico Traçamos uma
perpendicular à recta 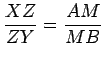 O ponto
Quando a recta se desloca mantendo-se sempre perpendicular a uma das
curvas, |
|||
|
Este resultado permite por exemplo calcular o centro de curvatura de
uma elipse como se ilustra no applet seguinte: Created with Cinderella |
|||
|
Aqui as curvas 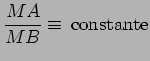 A
construção prossegue como atrás se indicou -
há que
colocar a perpendicular a 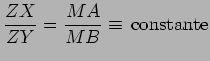 Compare com o seguinte applet, onde a
determinação do
centro (e
raio) de curvatura se faz através do círculo osculador
(que tem
contacto de ordem Created with Cinderella |
|
||
| |
Consideremos um
círculo móvel de centro
Created with Cinderella
Unamos o ponto
Os triângulos 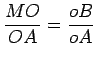
Nesta proporção os
segmentos Created with Cinderella
A semelhança dos triângulos
Podemos portanto construir o seu ponto característico A normal ao
epiciclóide no ponto De
acordo com a construção de Mannheim, para
construir o ponto
característico Podemos fazer a construção directa, como o fizemos para a elipse. No entanto, é mais fácil fazer o seguinte: A partir do
ponto Para ver que
de facto assim é, prolonguemos a recta
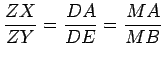
O ponto Esta construção deve-se a Euler e Savary. Resumindo:
Quando se pretende calcular o
centro de curvatura da
trajectória
de um ponto
|
||
|
Next: About this document ... Previous: 3-Barras Contents Joao Nuno Tavares 2005-05-20 |
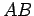 envolve uma curva dada
envolve uma curva dada
 . As extremidades
. As extremidades  e
e 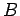 dessa recta movem-se, respectivamente, sobre as
curvas
dessa recta movem-se, respectivamente, sobre as
curvas 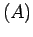 e
e 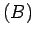 .
. 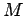 o outro vértice do triângulo
móvel (deformável)
o outro vértice do triângulo
móvel (deformável) 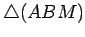 .
. 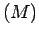 de
de 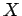 , está na intersecção da
normal em
, está na intersecção da
normal em 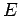 à envolvente
à envolvente
 , está na intersecção da
normal em
, está na intersecção da
normal em 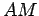 e
e 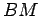 envolvem duas curvas e podemos calcular os
pontos característicos de contacto pelo processo habitual.
Assim, o ponto característico
envolvem duas curvas e podemos calcular os
pontos característicos de contacto pelo processo habitual.
Assim, o ponto característico 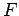 do lado
do lado 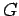 do lado
do lado 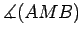 é o ponto
é o ponto 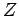 , onde as perpendiculares, consideradas
anteriormente, se intersectam.
, onde as perpendiculares, consideradas
anteriormente, se intersectam. 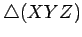 e
portanto:
e
portanto: 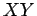 tomamos um ponto
tomamos um ponto 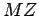 é a normal pedida.
é a normal pedida. 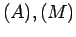 e
e 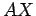 ,
, 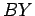 e
e 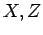 e
e 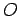 que
rola sem deslizar
sobre um outro círculo fixo de centro
que
rola sem deslizar
sobre um outro círculo fixo de centro 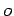 . O
ponto
. O
ponto 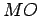 .
Esta recta
encontra a normal
.
Esta recta
encontra a normal 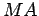 no
ponto
no
ponto 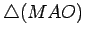 e
e
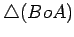 são
semelhantes e daí que:
são
semelhantes e daí que:
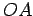 e
e 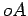 têm sempre
comprimento constante, qualquer que seja a posição do
círculo
móvel. Portanto o segmento
têm sempre
comprimento constante, qualquer que seja a posição do
círculo
móvel. Portanto o segmento 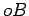 tem
também sempre o mesmo
comprimento, o que significa que
tem
também sempre o mesmo
comprimento, o que significa que 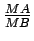 é sempre
constante. A recta
é sempre
constante. A recta 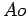 ; a normal ao
círculo concêntrico
; a normal ao
círculo concêntrico 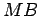 que seja dividida pelas normais atrás indicadas -
que seja dividida pelas normais atrás indicadas - 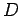 ; a
recta
; a
recta 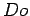 corta a normal
corta a normal 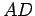 até ao
ponto
até ao
ponto 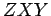 a
a 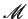 , num
movimento genérico
, num
movimento genérico 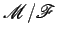 ,
procedemos da seguinte forma:
,
procedemos da seguinte forma:  ) a um movimento epicicloidal do tipo que
acabamos de analisar
) a um movimento epicicloidal do tipo que
acabamos de analisar