Como Newton e Feynman provam a lei das áreas.

A aproximação poligonal de Newton

Em 1687 Newton usou um método de aproximação poligonal para demonstrar a lei das áreas de Kepler, válida para qualquer força central.

Feynman retoma essencialmente o mesmo método na sua aula.

Proposição I de Newton

Seja um ponto fixo (Sol) e um ponto móvel (planeta). Suponhamos que a única força que actua em , em cada instante, é radial, isto é, tem a direcção da recta que une e , nesse instante.

Então:

a trajectória de é plana

o raio vector $\overrightarrow{SP}$ varre áreas iguais em intervalos de tempo iguais.

A aproximação poligonal
de Newton

Por favor habilite Java para uma construção interativa (com Cinderella).

Um corpo desloca-se da posição inicial 0 até à posição 1, com movimento uniforme de velocidade ${\bf v}_0$ , durante um intervalo de tempo $\Delta t$ . Portanto, a distância que ele percorre, ao ir da posição 0 para a posição 1 , é igual a:

$\displaystyle \hbox{dist}(0;1)= v_0 \times \Delta t$

Na posição 1 , o corpo (de massa 1) é sujeito à acção de uma força impulsiva ${\bf F}$ , dirigida para um centro de forças fixo $ S$ . A força actua durante um intervalo de tempo muito pequeno $\delta t$ . Portanto, a velocidade comunicada ao corpo por esta força é:

$\displaystyle {\bf w}_1={\bf F}\cdot \delta t$

Se o corpo estivesse em repouso na posição 1, ele deslocar-se-ia para a posição 1'' , indicada no applett, ao fim do intervalo de tempo $\Delta t$ , depois de percorrer uma distância igual a:

$\displaystyle {\bf w}_1\times \Delta t$
Se a força ${\bf F}$ não existisse, o corpo deslocar-se-ia por inércia atingindo um ponto 1', ao fim do mesmo intervalo de tempo $\Delta t$ , depois de percorrer uma distância igual a:

$\displaystyle {\bf v}_0\times \Delta t$

a partir da posição 1 (ver o applett).

Mas agora, na posição 1, o corpo está sujeito à lei de composição de velocidades. Pela regra do paralelogramo, a velocidade que ele adquire será:

$\displaystyle {\bf v}_1={\bf v}_0+{\bf w}_1$

e, ao fim do mesmo intervalo de tempo $\Delta t$ , ele atinge a posição 2 , na direcção de ${\bf v}_1$ e tal que:

$\displaystyle \hbox{dist}(1;2)= v_1\times \Delta t$

e assim sucessivamente ...

Este método é consecutivamente usado por Newton em toda a sua Dinâmica.

Lei das áreas

A prova da lei das áreas é agora elementar.

Por favor habilite Java para uma construção interativa (com Cinderella).
De facto, os triângulos SO1 e S12 têm a mesma área uma vez que eles têm a mesma base S1 e alturas iguais (porquê?).

Por favor habilite Java para uma construção interativa (com Cinderella).

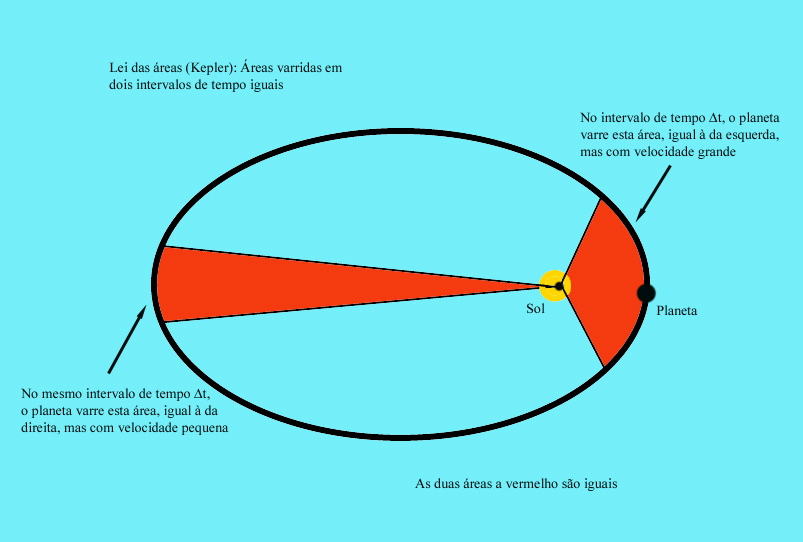
A lei das áreas diz que:

$\displaystyle \Delta t \propto (\hbox{\'area varrida})$

Uma consequência da lei das áreas, que será usada em breve, é a seguinte: o planeta move-se mais rapidamente quando está mais perto do Sol.

Por favor habilite Java para uma construção interativa (com Cinderella).

Página seguinte: A aula esquecida de Feynman (I)
Página anterior: Os problemas directo e inverso
Regresso ao Índice