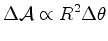A aula esquecida de Feynman (I)
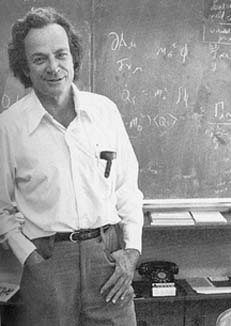 |
||
|
Feynman,
na sua "Lost lecture", resolve o problema inverso
relativo
à força central
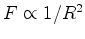 , isto é, conhecendo a força, ele prova a lei das elipses
de Kepler: ``Cada planeta move-se sobre
uma elipse com o sol num dos
focos" , usando argumentos de geometria elementar!
, isto é, conhecendo a força, ele prova a lei das elipses
de Kepler: ``Cada planeta move-se sobre
uma elipse com o sol num dos
focos" , usando argumentos de geometria elementar! Como vimos, Newton considera uma aproximação poligonal da órbita, constituída por uma série de pontos separados por um mesmo intervalo de tempo  . Em cada um desses pontos, a
trajectória do planeta é desviada do movimento
rectilíneo por
inércia por uma força impulsiva que o atrai em
direcção ao
Sol.
. Em cada um desses pontos, a
trajectória do planeta é desviada do movimento
rectilíneo por
inércia por uma força impulsiva que o atrai em
direcção ao
Sol. |
||
| A aproximação poligonal de Feynman | ||
Feynman
usa uma aproximação
poligonal diferente - os
vértices da poligonal em vez de estarem separados por um mesmo
intervalo de tempo, estão agora separados por um mesmo
ângulo ao
centro
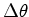 . .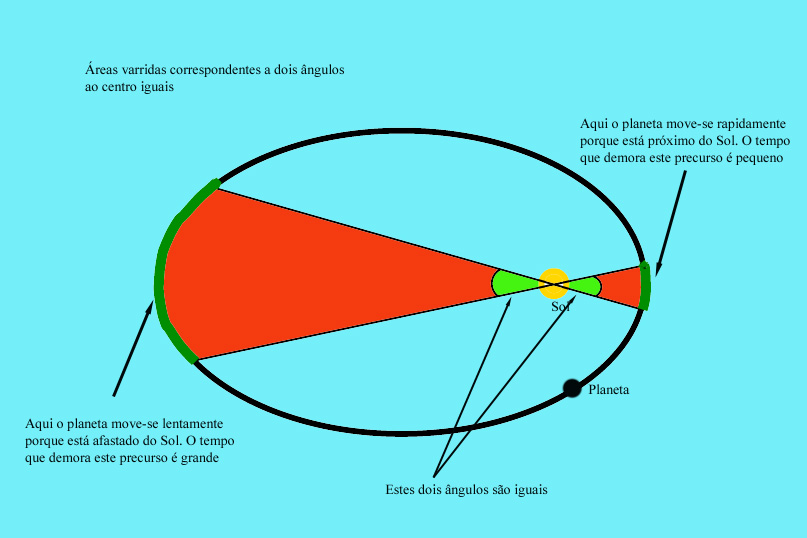 Na
figura acima os dois segmentos têm um mesmo ângulo ao
centro mas delimitam áreas diferentes e portanto correspondem a
tempos diferentes de percurso.
|
||
|
Do lado da órbita mais próximo do Sol o planeta vai de A para B , aí é desviado por 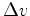 e continua de B para C. Do outro lado da
órbita, o planeta vai de D para E sofre
um novo impulso e segue de E para F, como se vê na figura
seguinte: e continua de B para C. Do outro lado da
órbita, o planeta vai de D para E sofre
um novo impulso e segue de E para F, como se vê na figura
seguinte: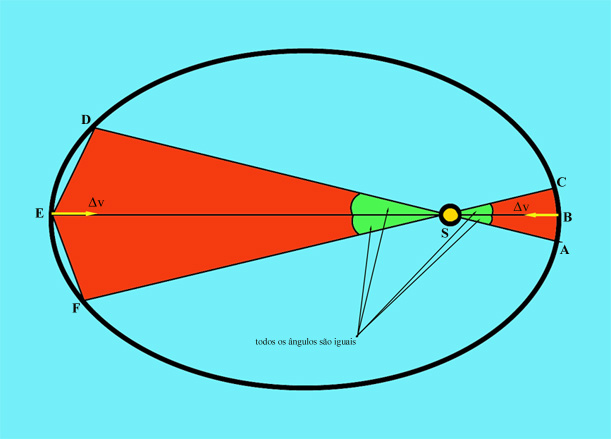 Sabemos
que o planeta move-se mais rapidamente ao longo de BC do
que ao longo de EF (recorde que, de acordo com a lei das áreas,
o planeta move-se mais rapidamente quando está mais perto do
Sol). Para saber quão mais rapidamente, temos que
comparar as áreas dos triângulos Goodstein em [2] mostra que a área é proporcional ao quadrado da distância do planeta ao Sol: 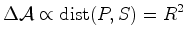 O argumento está explicado na figura
seguinte:
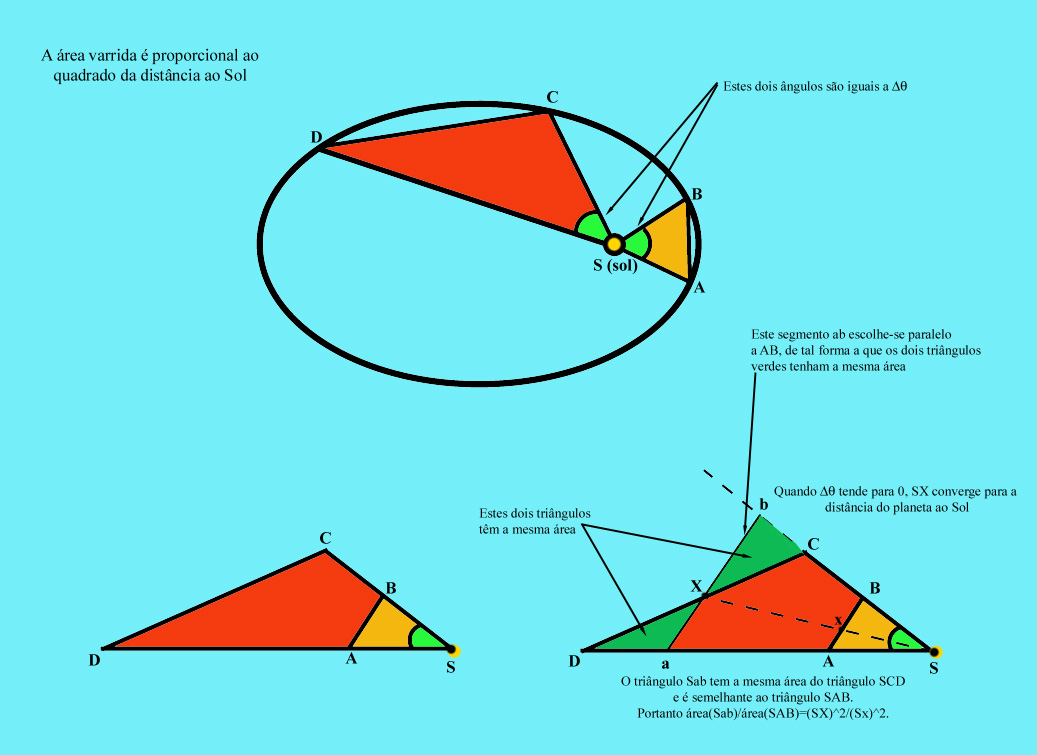 Mas um argumento de aproximação mostra, mais precisamente, que: 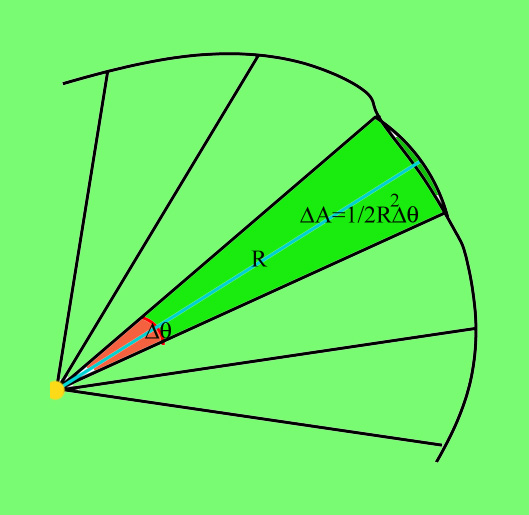 |
||
| Página
seguinte: A aula esquecida de Feynman (II) Página anterior: Como Newton e Feynman provam a lei das áreas Regresso ao Índice |
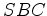 e
e 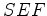 , uma vez que os
tempos são proporcionais às áreas (lei das
áreas de Kepler).
, uma vez que os
tempos são proporcionais às áreas (lei das
áreas de Kepler).