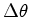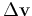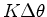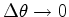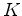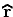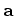|
O que é que
sabemos mais? Vejamos:
- A segunda lei de
Newton diz que:
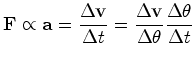 |
(4) |
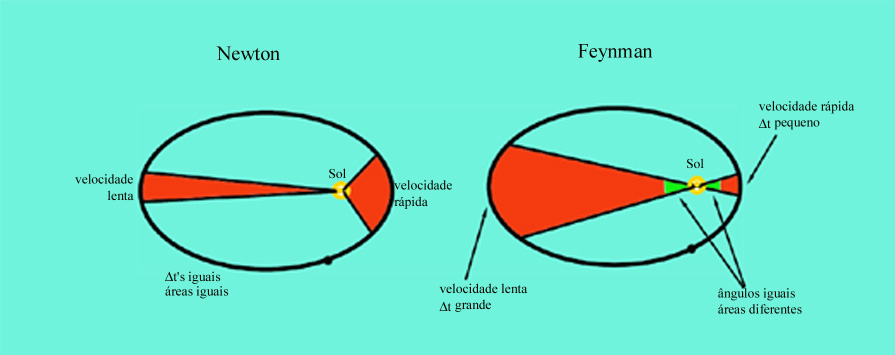
- A lei das
áreas diz que o tempo é proporcional à área:
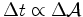 , e atendendo
a (3): , e atendendo
a (3):
isto é:
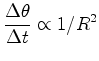 |
(5) |
- Por
hipótese,
conhecemos como a força central
depende de
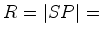 distância do planeta ao Sol - a força é a da
atracção universal de Newton -
força central inversamente proporcional ao quadrado da
distância:
distância do planeta ao Sol - a força é a da
atracção universal de Newton -
força central inversamente proporcional ao quadrado da
distância:
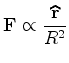 |
(6) |
onde 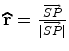 é
um vector unitário com a direcção do raio vector
do ponto é
um vector unitário com a direcção do raio vector
do ponto  ,
aplicado em
,
aplicado em  (o centro de forças). (o centro de forças).
Finalmente, reunindo toda esta
informação, temos
então que, por
(6), (4) e (5),
respectivamente:
o que implica que:
ou ainda:
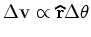 |
(7) |
Portanto:
a
variação da velocidade
é proporcional à
variação do ângulo e tem sempre a
direcção radial,
determinada pelo vector de posição.
Em
particular, 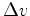 não depende de não depende de 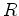 ! Em todo o ponto da órbita, não importa quão
distante ou perto do Sol, o
! Em todo o ponto da órbita, não importa quão
distante ou perto do Sol, o 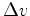 correspondente a um dado ângulo
é sempre o mesmo! Isto acontece porque, como vimos em (6),
à medida que o planeta se afasta do Sol, a força que
sobre ele actua fica cada vez mais fraca (diminui com o quadrado da
distância) mas o tempo que a força actua no planeta
aumenta (com o quadrado da distância, como em (3)).
O resultado é que
todos os correspondente a um dado ângulo
é sempre o mesmo! Isto acontece porque, como vimos em (6),
à medida que o planeta se afasta do Sol, a força que
sobre ele actua fica cada vez mais fraca (diminui com o quadrado da
distância) mas o tempo que a força actua no planeta
aumenta (com o quadrado da distância, como em (3)).
O resultado é que
todos os 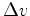 's são iguais.
's são iguais.
|
|
|
Este
é o resultado
principal de Feynman. Ele
permite reconstruir a
aproximação poligonal da órbita, dados:
- 1.
- a posição inicial 0 do
planeta
- 2.
- a sua velocidade inicial
 e ainda e ainda
- 3.
- o
valor constante de
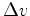
De facto, como se pode
ver no applett seguinte:
- o
planeta, partindo de 0, segue em linha
recta com movimento
uniforme com velocidade
 . Quando o raio vector varre um
ângulo ao centro de
. Quando o raio vector varre um
ângulo ao centro de 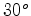 , o planeta atinge o ponto 1.
, o planeta atinge o ponto 1.
- no
ponto 1 o planeta sofre uma força impulsiva que muda a
sua velocidade de
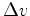 no sentido radial. A nova velocidade no sentido radial. A nova velocidade  é calculada pela
regra do paralelogramo é calculada pela
regra do paralelogramo 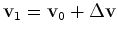 .
.
- o planeta, partindo de 1, segue com
movimento
rectilíneo
uniforme com velocidade
 . Quando o raio vector varre um
ângulo ao centro de
. Quando o raio vector varre um
ângulo ao centro de 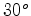 , o planeta atinge o ponto 2.
, o planeta atinge o ponto 2.
- no
ponto 2 o planeta sofre uma força impulsiva que muda a
sua velocidade de
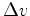 no sentido radial. A nova velocidade no sentido radial. A nova velocidade 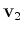 é calculada pela
regra do paralelogramo é calculada pela
regra do paralelogramo 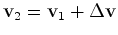 .
.
e assim sucessivamente.
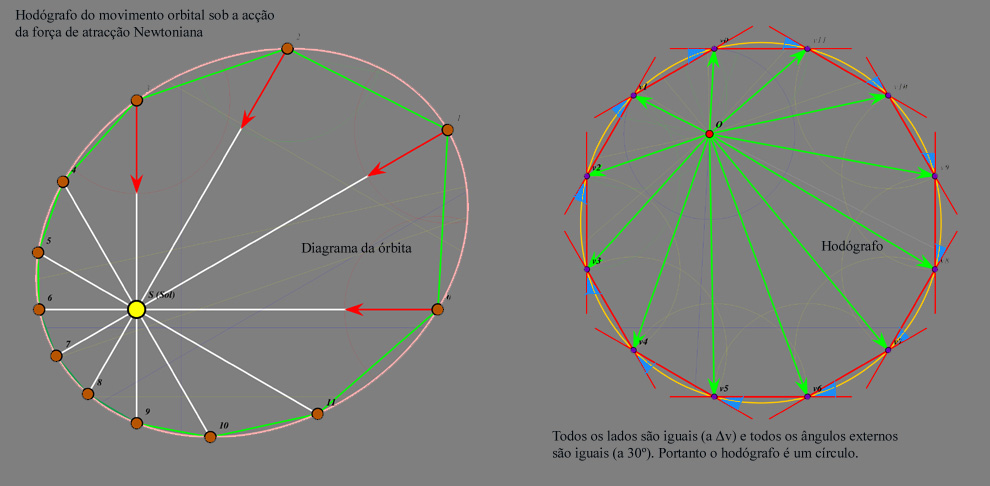
No
applett seguinte
destacou-se, num diagrama separado, a variação sucessiva
das velocidades. A este diagrama de
velocidades
chama-se hodógrafo (=
graphein + hodos = desenhar o
caminho). Foi
inventado por Hamilton.
Como acabamos de deduzir, o
hodógrafo para o movimento de um
planeta sob a acção de um campo de atracção
Newtoniano, é um
círculo, cujo centro 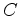 em geral não coincide com a origem em geral não coincide com a origem 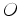 do hodógrafo.
do hodógrafo.
Se dividirmos a
trajectória em sectores que subentendem ângulos
iguais 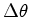 (por exemplo
iguais a (por exemplo
iguais a 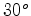 , como no applett),
então a soma de todos os
, como no applett),
então a soma de todos os 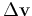 's formam um polígono
regular uma vez que as sucessivas mudanças dos vectores
velocidade estão inclinadas umas relativamente às outras
de um
mesmo ângulo
's formam um polígono
regular uma vez que as sucessivas mudanças dos vectores
velocidade estão inclinadas umas relativamente às outras
de um
mesmo ângulo 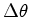 , e todos os
, e todos os 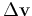 's têm o mesmo
tamanho,
's têm o mesmo
tamanho, 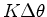 . No limite, quando
. No limite, quando 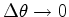 , o
polígono torna-se um círculo de raio
, o
polígono torna-se um círculo de raio 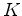 . O centro do círculo
é o ponto de onde parte
. O centro do círculo
é o ponto de onde parte 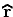 . De facto, a "velocidade" do
hodógrafo, tangente ao círculo, é a
aceleração
. De facto, a "velocidade" do
hodógrafo, tangente ao círculo, é a
aceleração 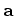 .
.
|
|

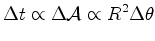
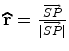 é
um vector unitário com a direcção do raio vector
do ponto
é
um vector unitário com a direcção do raio vector
do ponto  ,
aplicado em
,
aplicado em  (o centro de forças).
(o centro de forças).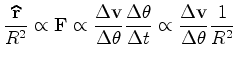
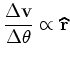
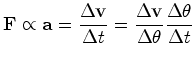
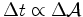 , e atendendo
a (
, e atendendo
a (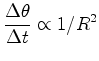
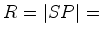 distância do planeta ao Sol - a força é a da
atracção universal de Newton -
força central inversamente proporcional ao quadrado da
distância:
distância do planeta ao Sol - a força é a da
atracção universal de Newton -
força central inversamente proporcional ao quadrado da
distância: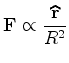
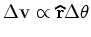
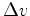 não depende de
não depende de 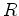 ! Em todo o ponto da órbita, não importa quão
distante ou perto do Sol, o
! Em todo o ponto da órbita, não importa quão
distante ou perto do Sol, o 
 e ainda
e ainda 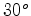 , o planeta atinge o ponto 1.
, o planeta atinge o ponto 1. é calculada pela
regra do paralelogramo
é calculada pela
regra do paralelogramo 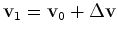 .
. 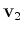 é calculada pela
regra do paralelogramo
é calculada pela
regra do paralelogramo 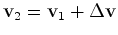 .
. 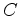 em geral não coincide com a origem
em geral não coincide com a origem 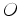 do hodógrafo.
do hodógrafo.