 |
||
|
Hamilton inventou o
hodógrafo como uma nova maneira de pensar uma
trajectória - um ponto do hodógrafo representa o vector
velocidade num certo instante e portanto o hodógrafo representa
a
variação do vector velocidade com o tempo - o arco de
hodógrafo
entre dois instantes infinitamente próximos é
proporcional
à
aceleração. Por outras palavras, a "velocidade" do
hodógrafo
representa a aceleração do corpo. 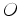 e, para cada instante
e, para cada instante 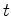 , desenhamos o vector
, desenhamos o vector 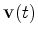 |
||
| Reconstrução
da órbita |
||
|
O
problema que surge agora é que,
embora
saibamos através do hodógrafo, a direcção e
grandeza
do vector
velocidade, não sabemos em que ponto do plano (pertencente
à
órbita) é que ele é tangente? Não sabemos
pois onde
colocá-lo. O hodógrafo continua um
círculo mas agora todos os raios do hodógrafo são
perpendiculares às verdadeiras direcções das
velocidades. Mas isto é exactamente o que acontece na
construção acima referida. O tamanho da
trajectória não fica
determinado mas,
pelo menos, a sua forma será a correcta. Vejamos como (veja o applett anterior).
Para
calcular o comprimento do vector velocidade desenhamos um
hodógrafo auxiliar, como se indica no applett anterior.
Consegue provar que de facto assim acontece , isto é, que quando 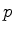 varia sobre o
hodógrafo varia sobre o
hodógrafo  descreve uma elipse? Clique aqui. descreve uma elipse? Clique aqui.E quando S está fora do círculo? E quando está sobre? |
||
| Referências | |
|
| |
|
|
|
Última
actualização: 20 de Maio de 2006
|
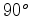 graus, no sentido
horário.
graus, no sentido
horário. 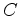 , como sabemos, e
com uma origem arbitrária
, como sabemos, e
com uma origem arbitrária 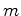 do segmento
do segmento 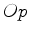 .
.
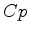 , que une
, que une