Ao conjunto:
chama-se cónica com excentricidade
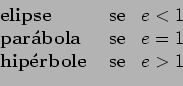
![]() .
.
FIGURA
Uma das possíveis definições de cónica, é a seguinte:
Ao conjunto:

![]() .
.
APPLET CINDERELLA
Consideremos um sistema de eixos cartesianos cuja origem coincide
com o foco ![]() , com o eixo dos
, com o eixo dos ![]() perpendicular à directriz,
como na figura seguinte:
perpendicular à directriz,
como na figura seguinte:
FIGURA ConicasCoordPolares.jpg
Com as notações seguintes:
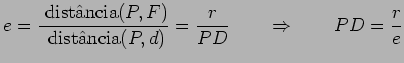
Mas, por outro lado:
Portanto, nesta situação, virá que:
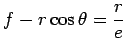
Resolvendo em ordem a ![]() , obtem-se:
, obtem-se:
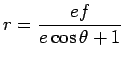
Supondo que ![]() está à direita da directriz,
como na figura, de tal forma que agora
está à direita da directriz,
como na figura, de tal forma que agora
![]() , deduzimos, de
forma análoga, que:
, deduzimos, de
forma análoga, que:
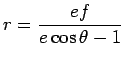
FIGURA ConicasCoordPolares2.jpg
Resumindo:
Seja
![]() uma cónica com excentricidade
uma cónica com excentricidade ![]() , foco
, foco ![]() na origem
das coordenadas, e com uma directriz vertical
na origem
das coordenadas, e com uma directriz vertical ![]() , situada à
direita do foco, a uma deste igual a
, situada à
direita do foco, a uma deste igual a ![]() .
.
Se ![]() , a cónica
, a cónica
![]() é uma elipse ou uma parábola.
Todo o ponto
é uma elipse ou uma parábola.
Todo o ponto ![]() de
de
![]() está à esquerda da directriz e
satisfaz equação polar:
está à esquerda da directriz e
satisfaz equação polar: