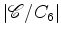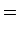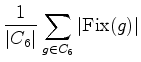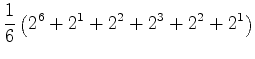|
- Regressemos ao problema de
calcular
o número de padrões
distintos de
um hexágono regular, cujos vértices estão
coloridos apenas com duas cores - B (branco) e P (preto).
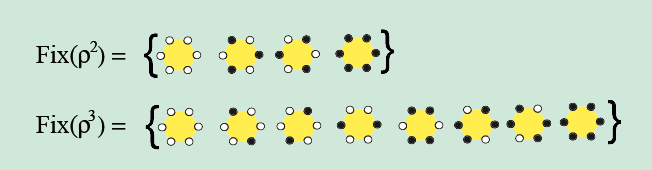
Como veremos,
é muito importante
calcular o conjunto dos pontos
fixos, 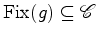 , de cada
, de cada 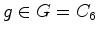 , e, para isso,
convem ter a representação dos elementos de
, e, para isso,
convem ter a representação dos elementos de 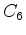 , como
permutações dos vértices do hexágono, e
ainda as correspondentes
decomposições num produto de ciclos disjuntos:
, como
permutações dos vértices do hexágono, e
ainda as correspondentes
decomposições num produto de ciclos disjuntos:
Por exemplo, no cálculo de
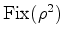 usamos o
facto de que
usamos o
facto de que
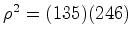 e, portanto,
qualquer
coloração e, portanto,
qualquer
coloração 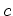 que fique
fixa por que fique
fixa por 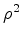 , tem que ter os vértices
, tem que ter os vértices 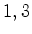 e e 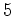 da mesma côr.
Analogamente os vértices da mesma côr.
Analogamente os vértices 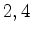 e e 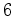 têm que ter
também a mesma
côr. têm que ter
também a mesma
côr.
Portanto
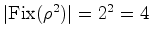 , onde o 2 da base se refere ao
número de cores (apenas duas neste caso - branco e preto) e o
expoente ao número de ciclos de
, onde o 2 da base se refere ao
número de cores (apenas duas neste caso - branco e preto) e o
expoente ao número de ciclos de 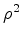 - dois.
- dois.
De facto:
|
|
|
Demonstração
...
Quantas vezes é que uma dada
``coloração, 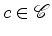 entra na
soma entra na
soma 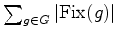 ?
?
É claro que 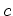 entra cada vez que existe um entra cada vez que existe um 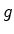 que
deixa que
deixa 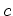 fixo.
Portanto, fixo.
Portanto, 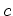 entra na soma tantas vezes
quantas o cardinal entra na soma tantas vezes
quantas o cardinal
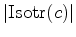 do
subgrupo de isotropia de do
subgrupo de isotropia de 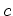 .
.
Todas as colorações
que
estão na mesma órbita de 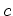 entram na soma
o mesmo número de vezes uma vez que todos os seus
estabilizadores
têm o mesmo
entram na soma
o mesmo número de vezes uma vez que todos os seus
estabilizadores
têm o mesmo
cardinal. Portanto, a
contribuição da
órbita de 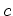 é é
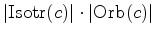 que,
pela fórmula (4),
é igual
a: que,
pela fórmula (4),
é igual
a:
Vemos pois que cada órbita
dá a mesma
contribuição 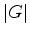 , para a
soma
, para a
soma 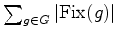 . A soma total é portanto
. A soma total é portanto 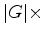 número de órbitas
número de órbitas 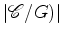 , isto é:
, isto é:
que é exactamente a
igualdade
que se
pretendia provar.

|
|
|
Assim, pelo lema de Burnside, o
número de padrões distintos de um
hexágono regular, cujos vértices estão coloridos
apenas com duas cores - B (branco) e P (preto) é igual a:
como aliás já
sabíamos!
|
|
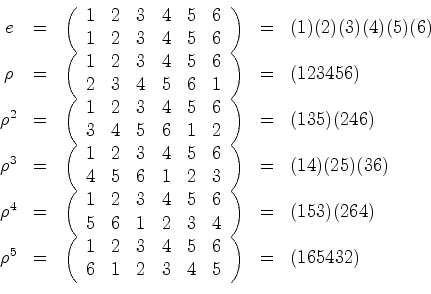
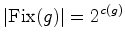
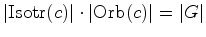
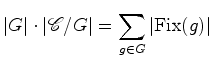

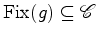 , de cada
, de cada 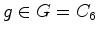 , e, para isso,
convem ter a representação dos elementos de
, e, para isso,
convem ter a representação dos elementos de 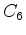 , como
permutações dos vértices do hexágono, e
ainda as correspondentes
decomposições num produto de ciclos disjuntos:
, como
permutações dos vértices do hexágono, e
ainda as correspondentes
decomposições num produto de ciclos disjuntos: 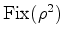 usamos o
facto de que
usamos o
facto de que
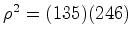 e, portanto,
qualquer
coloração
e, portanto,
qualquer
coloração 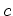 que fique
fixa por
que fique
fixa por 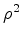 , tem que ter os vértices
, tem que ter os vértices 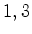 e
e 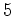 da mesma côr.
Analogamente os vértices
da mesma côr.
Analogamente os vértices 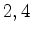 e
e  têm que ter
também a mesma
côr.
têm que ter
também a mesma
côr. 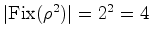 , onde o 2 da base se refere ao
número de cores (apenas duas neste caso - branco e preto) e o
expoente ao número de ciclos de
, onde o 2 da base se refere ao
número de cores (apenas duas neste caso - branco e preto) e o
expoente ao número de ciclos de 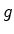 - os vértices que
ocorrem em cada
ciclo de
- os vértices que
ocorrem em cada
ciclo de 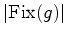 fica
determinado pelo número
fica
determinado pelo número 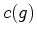 de ciclos de
de ciclos de 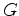 um grupo que actua
num conjunto
um grupo que actua
num conjunto 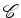 (ambos finitos).
(ambos finitos). 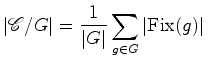
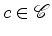 entra na
soma
entra na
soma 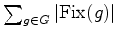 ?
? 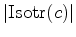 do
subgrupo de isotropia de
do
subgrupo de isotropia de 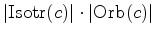 que,
pela fórmula (
que,
pela fórmula (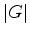 , para a
soma
, para a
soma 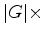 número de órbitas
número de órbitas 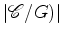 , isto é:
, isto é: